Các câu hỏi tương tự
Đặt
a
ln
2
,
b
ln
5
, hãy biểu diễn
I
ln
1
2
+
ln
2
3
+
.
.
.
+
ln
98
99
+
ln
99
100
theo a và b. A.
I
-...
Đọc tiếp
Đặt a = ln 2 , b = ln 5 , hãy biểu diễn I = ln 1 2 + ln 2 3 + . . . + ln 98 99 + ln 99 100 theo a và b.
A. I = - 2 a - b
B. I = 2 a + b
C. I = - 2 a + b
D. I = 2 a - b
Câu 1:(0,5đ)Liệt kê các phần tử của tập hợp A {x ∈ N/15 ≤ x ≤ 19}Câu 2: (3đ) thực hiện phép tínha. 2.(72 – 2.32) – 60b. 27.63 + 27.37c. l-7l + (-8) + l-11l + 2d. 568 – 34 {5.l9 – ( 4-1)2l + 10}Câu 3: ( 2,5 điểm ) Tìm số nguyên xa) 2x + 3 52 : 5b) 105 – ( x + 7) 27 : 25Câu 4 (1 điểm): Học sinh lớp 6B khi xếp hàng 2, hàng 4, hàng 8 đều vừa đủ hàng. Biết số học sinh lớp đó trong khoảng 30 đến 38. Tính số học sinh của lớp 6B.Câu 5:(1 điểm) Khi nào thì M là trung điểm của đoạn thẳng AB? Vẽ...
Đọc tiếp
Câu 1:(0,5đ)
Liệt kê các phần tử của tập hợp A = {x ∈ N/15 ≤ x ≤ 19}
Câu 2: (3đ) thực hiện phép tính
a. 2.(72 – 2.32) – 60
b. 27.63 + 27.37
c. l-7l + (-8) + l-11l + 2
d. 568 – 34 {5.l9 – ( 4-1)2l + 10}
Câu 3: ( 2,5 điểm ) Tìm số nguyên x
a) 2x + 3 = 52 : 5
b) 105 – ( x + 7) = 27 : 25
Câu 4 (1 điểm): Học sinh lớp 6B khi xếp hàng 2, hàng 4, hàng 8 đều vừa đủ hàng. Biết số học sinh lớp đó trong khoảng 30 đến 38. Tính số học sinh của lớp 6B.
Câu 5:(1 điểm) Khi nào thì M là trung điểm của đoạn thẳng AB? Vẽ hình minh họa.
Câu 6: ( 2 điểm )Vẽ tia Ox, trên Ox lấy điểm A và B sao cho OA= 4cm, OB = 8cm.
a. Trong 3 điểm O, A, B điểm nào nằm giữa 2 điểm còn lại. Vì sao? . So sánh OA và AB
b. A có phải là trung điểm của OB không? Vì sao ?
Cho
log
2
a
,
log
3
b
. Biểu diễn
log
625
270
theo a và b là: A.
1
4
3
b
+
1
1
-
a
B....
Đọc tiếp
Cho log 2 = a , log 3 = b . Biểu diễn log 625 270 theo a và b là:
A. 1 4 3 b + 1 1 - a
B. a + 2 b 2 3 a 1 - b
C. a + b 2 4 a 1 - b
D. a + b 2 2 a 1 - b
Gọi L là chiều dài của đoạn đường có điểm đầu là A và điểm cuối B (hình vẽ là những nửa đường tròn đồng tâm O và có bán kính lần lượt là 1, 2, 3, 4, 5). Hãy chọn khẳng định đúng. A. 51 B. L 52 C. 47 D. L 50
Đọc tiếp
Gọi L là chiều dài của đoạn đường có điểm đầu là A và điểm cuối B (hình vẽ là những nửa đường tròn đồng tâm O và có bán kính lần lượt là 1, 2, 3, 4, 5). Hãy chọn khẳng định đúng.
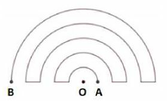
A. 51
B. L > 52
C. 47
D. L < 50
Đặt
a
log
2
5
,
b
log
3
5
. Hãy biểu diễn log 6 5 theo a và b. A.
log
6
5
1
a
+
b
B.
log
6
5
a...
Đọc tiếp
Đặt a = log 2 5 , b = log 3 5 . Hãy biểu diễn log 6 5 theo a và b.
A. log 6 5 = 1 a + b
B. log 6 5 = a b a + b
C. log 6 5 = a 2 + b 2
D. log 6 5 = a + b
Cho số phức za+bi, a,b ÎR. Tìm điều kiện của a và b để điểm biểu diễn z thuộc hình tròn tâm O bán kính R 3 như hình vẽ bên A.
a
2
+
b
2
9
B.
-
3
≤
a
≤
3
-
3...
Đọc tiếp
Cho số phức z=a+bi, a,b ÎR. Tìm điều kiện của a và b để điểm biểu diễn z thuộc hình tròn tâm O bán kính R = 3 như hình vẽ bên
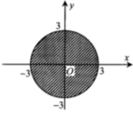
A. a 2 + b 2 > 9
B. - 3 ≤ a ≤ 3 - 3 ≤ b ≤ 3
C. a 2 + b 2 ≤ 9
D. a < - 3 b > 3
Đặt log126a và log127b Hãy biểu diễn log27 theo a và b A.
log
2
7
a
1
-
b
B.
log
2
7
a
1
+
b
C.
log
2
7
b
1...
Đọc tiếp
Đặt log126=a và log127=b Hãy biểu diễn log27 theo a và b
A. log 2 7 = a 1 - b
B. log 2 7 = a 1 + b
C. log 2 7 = b 1 - a
D. log 2 7 = a a - 1
Đặt
a
log
3
5
,
b
log
4
5
. Hãy biểu diễn
log
15
10
theo a và b. A.
log
15
10
a
2
-
a
b
a...
Đọc tiếp
Đặt a = log 3 5 , b = log 4 5 . Hãy biểu diễn log 15 10 theo a và b.
A. log 15 10 = a 2 - a b a b + b
B. log 15 10 = a + 2 a b 2 a b + 2 b
C. log 15 10 = a + 2 a b 2 a b
D. log 15 10 = a 2 - a b a b
Đặt
log
7
12
a
,
log
12
24
b
.
Hãy biểu diễn
log
54
168
theo a và b. A.
ab
+
1
8...
Đọc tiếp
Đặt log 7 12 = a , log 12 24 = b . Hãy biểu diễn log 54 168 theo a và b.
A. ab + 1 8 a − b
B. ab + 1 8 a + 5 b
C. ab − 1 a 5 − 8 b
D. ab + 1 a 8 − 5 b





