B=(1/4.9+1/9.14+...+1/44.49).1-3-5-...-49/89
B=1/5(1/4-1/9+1/9-1/14+...+1/44-1/49).1-(3+5+...+49)/89
B=1/5(1/4-1/49).1-24.52:2/89
B=9/196.-7
B=-9/28
Ta có \(\frac{1-3-5-..-49}{89}=\frac{1-\left(3+5+7+...+49\right)}{89}\)
\(=\frac{1-\left[\left(49-3\right):2+1\right].\left(\frac{49+3}{2}\right)}{89}=\frac{1-624}{89}=-7\)
Lại có \(\frac{1}{4.9}+\frac{1}{9.14}+....+\frac{1}{44.49}=\frac{1}{5}\left(\frac{5}{4.9}+\frac{5}{9.14}+...+\frac{5}{44.49}\right)\)
\(=\frac{1}{5}\left(\frac{1}{4}-\frac{1}{9}+\frac{1}{9}-\frac{1}{14}+...+\frac{1}{44}-\frac{1}{49}\right)=\frac{1}{5}\left(\frac{1}{4}-\frac{1}{49}\right)=\frac{1}{5}.\frac{45}{196}=\frac{9}{196}\)
Khi đó \(B=\frac{9}{196}.\left(-7\right)=-\frac{9}{28}\)
\(B=\left(\frac{1}{4.9}+\frac{1}{9.14}+....+\frac{1}{44.49}\right).\left(\frac{1-3-5...-49}{89}\right)\)
\(B=\left[\left(\frac{5}{4.9}+\frac{5}{9.14}+...+\frac{5}{44.49}\right).\frac{1}{5}\right].\frac{1-3-5-...-49}{89}\)
\(B=\left[\left(\frac{1}{4}-\frac{1}{49}\right).\frac{1}{5}\right].\frac{1-3-5-...-49}{89}\)
\(B=\left[\frac{45}{196}.\frac{1}{5}\right].\frac{1-3-5-....-49}{89}\)
\(B=\frac{9}{196}.\frac{1-3-5-..-49}{86}\)
\(B=\frac{9}{196}.\frac{1-3-5-...-49}{2}\)
\(B=-\frac{801}{2408}\)
B=\((\frac{1}{4}\)\(-\)\(\frac{1}{9}\)\(+\)\(\frac{1}{9}\)\(-\)\(\frac{1}{14}\)+...+\(\frac{1}{44}\)-\(\frac{1}{49}\)\()\).(\(\frac{1-3-5-...-49}{89}\)
B=(\(\frac{1}{4}\)-\(\frac{1}{49}\)).\(\frac{-2+2...-2}{89}\)
B=(\(\frac{1}{4}\)-\(\frac{1}{49}\)).\(\frac{0}{89}\)
B=(\(\frac{1}{4}\)-\(\frac{1}{49}\)).0
B=0









 giúp mình với, mk cần gấp ạ, cảm ơn mn rất nhìu !
giúp mình với, mk cần gấp ạ, cảm ơn mn rất nhìu !


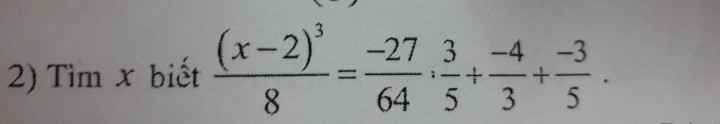








 Giúp em bài này được không ạ! e cảm ơn nhìu ạ
Giúp em bài này được không ạ! e cảm ơn nhìu ạ