Chọn A
Chú ý : Nnhieeuf học sinh áp dụng công thức tính đaoh hàm của một thương là không cần thiết vì biến không ở mẫu. Viết f(x) dạng trên, ta có ngay kết quả.
1. Mệnh đề nào dưới đây sai ?
A. Hàm số y = tan x là hàm số lẻ. B. Hàm số y = sin x là hàm số lẻ
C. Hàm số y = Cot x là hàm số lẻ D. Hàm số y = Cos x là hàm số lẻ
2. Hàm số nào sau đây là hàm số lẻ?
A. y = Cos3x B. y = Sinx + Cos3x
C. y = Sinx + Tan3x D. Tan2x
3. Trong các hàm số sau, hàm số nào là hàm số chẵn
A. y = Cos2x B. y = Cot2x
C. y = tan2x D. y = sin2x
4. Trong các hàm số sau, hàm số nào là hàm số lẻ?
A. y = Sinx Cos3x
B. y = Cosx + Sin2x
C. y = Cosx + Sinx
D. y = - Cosx
5. Hàm số nào là hàm số chẵn ?
A. y = Cosx
B. y = Sin x/2
C. y = tan2x
D. y = Cotx
Cho a,b,c,d là các số thực khác 0 và hàm số
y=f(x)= asincx + bcosdx. Khẳng định nào sau đây là đúng?
A. y=f(x)= asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi c d là số hữu tỉ.
B. y=f(x)= asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi a d là số hữu tỉ.
C. y=f(x)= asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi c b là số hữu tỉ.
D. y=f(x)= asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi a x là số hữu tỉ.
Cho hàm số y = f x = a x 5 + b x 3 + c x + d a , b , c , d ∈ ℝ ; a ≠ 0 . Biết f'(-1)=3 . Tính lim ∆ x → 0 f 1 + ∆ x - f 1 ∆ x
A. 3
B. -3
C. 1
D. -1
Cho hàm số \(y=-x^2+3x-2\) có đồ thị (D) a;Tính đạo hàm của hàm số tại điểm y',\(x_0\) thuộc R b,Viết phương trình tiếp tuyến của (P) tại điểm có hoành độ \(x_0=2\) c,Viết phương trình tiếp tuyến của (P) tại điểm có tung độ \(y_0=0\); d, Viết phương trình tiếp tuyến của (P) biết tiếp tiếp vuông góc với đường thẳng y'=x+3
Cho hàm số f ( x = x 3 + b x 2 + c x + d , C g x = x 2 - 3 x + 1
Với các số b, c, d tìm được ở bài 19, hãy:
a) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = - 1 .
b) Giải phương trình f ' sin x = 0 .
c) tính lim x → 0 f ' ' sin 5 x + 1 g ' sin 3 x + 3
Trong các hàm số sau đây, hàm số nào là hàm tuần hoàn?
A. y=tanx+x
B. y=x2+1
C. y=cotx
D. y=\(\dfrac{\text{sinx}}{x}\)
Hàm số y=f(x) xác định trên (c;d). Hàm số y=f(x) liên tục tại a€ (c;d) nếu
A.lim f(x)=-f(a)
B.lim f(x) # -f(a)
C.lim f(x) # f(a)
D.lim f(x)=f(a)
Cho các hàm số
f ( x ) = x 3 + b x 2 + c x + d ( C )
g ( x ) = x 2 − 3 x − 1 .
a) Xác định b, c, d sao cho đồ thị (C) đi qua các điểm (1; 3), (−1; −3) và f′(1/3) = 5/3 ;
b) Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ x 0 = 1 ;
c) Giải phương trình f′(sint) = 3;
d) Giải phương trình f′′(cost) = g′(sint);
e) Tìm giới hạn lim z → 0 f ' ' sin 5 z + 2 g ' sin 3 z + 3
Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.
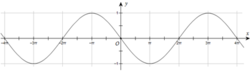
Hỏi hàm số đó là hàm số nào?
A. y = sin x 2 .
B. y = cos x 2 .
C. y = − cos x 4 .
D. y = sin − x 2 .
