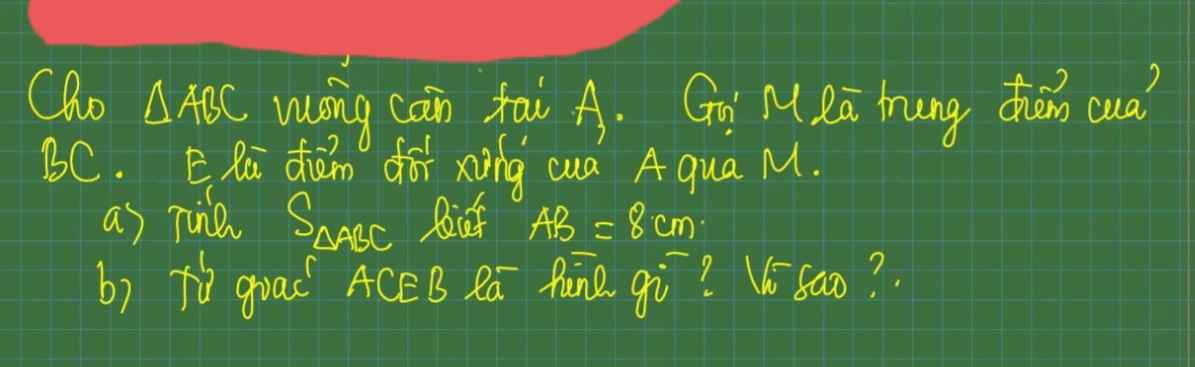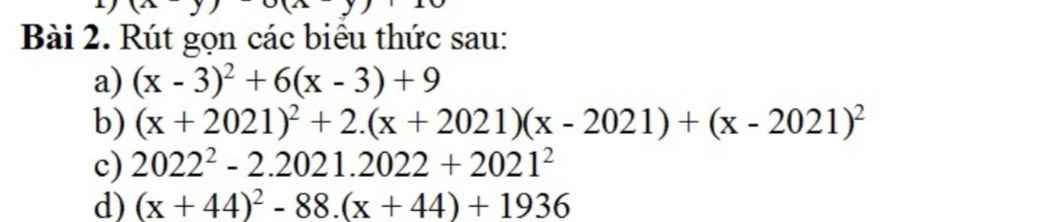- Ta có: AK=KI=IK mà AK+KI+IK=AH.
=>\(AK=KI=IK=\dfrac{1}{3}AH\);\(AI=KH=\dfrac{2}{3}BC\)
a)
- Xét tam giác ABH có:
MI//BH (gt)
=>\(\dfrac{AM}{AB}=\dfrac{AI}{AH}=\dfrac{2}{3}\)(định lí Ta-let)
- Xét tam giác ABC có:
MN//BC (gt)
=>\(\dfrac{AM}{AB}=\dfrac{MN}{BC}=\dfrac{2}{3}\) (định lí Ta-let)
=>PQ=\(\dfrac{2}{3}BC=\dfrac{2}{3}.27=18\) (cm)
b)- Xét tam giác ABH có:
PK//BH (gt)
=>\(\dfrac{AP}{AB}=\dfrac{AK}{AH}=\dfrac{1}{3}\)(định lí Ta-let)
- Xét tam giác ABC có:
PQ//BC (gt)
=>\(\dfrac{AP}{AB}=\dfrac{PQ}{BC}=\dfrac{1}{3}\) (định lí Ta-let)
=>PQ=\(\dfrac{1}{3}BC=\dfrac{1}{3}.27=9\) (cm)
c) SABC=\(\dfrac{1}{2}AH.BC\)=360cm2 (gt)
=>AH=\(\dfrac{2.360}{BC}=26,\left(6\right)\approx26,5\)(cm)
=>KI=\(\dfrac{1}{3}.26,5=8,8\left(3\right)\approx8,8\)(cm)
- Ta có: PQ//BC ; MN//BC (gt) nên PQ//MN
=>MNQP là hình thang
=>SMNPQ=\(\dfrac{\left(PQ+MN\right).KI}{2}=\dfrac{\left(18+9\right).8,8}{2}=118,8\)(cm2)