a: Xét ΔEAB và ΔECM có
\(\widehat{EAB}=\widehat{ECM}\)(hai góc so le trong, AB//MC)
\(\widehat{AEB}=\widehat{CEM}\)
Do đó: ΔEAB đồng dạng với ΔECM
=>\(\dfrac{EA}{EC}=\dfrac{AB}{CM}=\dfrac{AB}{\dfrac{CD}{2}}=\dfrac{2BA}{CD}\)
b: Ta có; ΔEAB đồng dạng với ΔECM
=>\(\dfrac{EB}{EM}=\dfrac{AB}{CM}\)
=>\(\dfrac{EM}{EB}=\dfrac{MC}{AB}=\dfrac{MD}{AB}\left(1\right)\)
Xét ΔFAB và ΔFMD có
\(\widehat{FAB}=\widehat{FMD}\)
\(\widehat{AFB}=\widehat{MFD}\)
Do đó: ΔFAB đồng dạng vớiΔFMD
=>\(\dfrac{FB}{FD}=\dfrac{AB}{MD}=\dfrac{FA}{FM}\)
=>\(\dfrac{FD}{FB}=\dfrac{MD}{AB};\dfrac{FM}{FA}=\dfrac{MD}{AB}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{FM}{FA}=\dfrac{EM}{FB}\)
Xét ΔMAB có \(\dfrac{MF}{FA}=\dfrac{ME}{EB}\)
nên FE//AB
Ta có: FE//AB
AB//CD
Do đó: FE//CD
c: Xét ΔCAB có EG//AB
nên \(\dfrac{EG}{AB}=\dfrac{CE}{CA}\left(3\right)\)
Xét ΔDAB có FH//AB
nên \(\dfrac{FH}{AB}=\dfrac{DF}{DB}\left(4\right)\)
Xét ΔMAB có FE//AB
nên \(\dfrac{FE}{AB}=\dfrac{ME}{MB}\left(5\right)\)
Ta có: ΔEAB đồng dạng với ΔECM
=>\(\dfrac{AE}{CE}=\dfrac{EB}{ME}\)
=>\(\dfrac{AE}{CE}+1=\dfrac{EB}{ME}+1\)
=>\(\dfrac{AE+CE}{CE}=\dfrac{EB+ME}{ME}\)
=>\(\dfrac{AC}{CE}=\dfrac{MB}{ME}\)
=>CE/CA=ME/MB(6)
Từ (3);(5);(6) suy ra EG/AB=EF/AB
=>EG=EF
Xét ΔBDM có FE//DM
nên \(\dfrac{BF}{DF}=\dfrac{BE}{EM}\)
=>\(\dfrac{BF+DF}{DF}=\dfrac{BE+EM}{EM}\)
=>\(\dfrac{BD}{DF}=\dfrac{BM}{EM}\)
=>\(\dfrac{DF}{BD}=\dfrac{EM}{BD}\left(7\right)\)
Từ (4),(5),(7) suy ra FH=FE
mà EG=EF
nên EG=EF=FH

 đag cần gấp
đag cần gấp



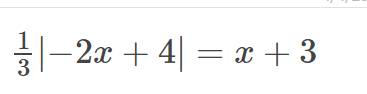 giúp mình với, đag cần gấp
giúp mình với, đag cần gấp

 giúp mik vs mik đag cần gấp
giúp mik vs mik đag cần gấp



 Giúp mik bài 4 vs mn, mik đag cần gấp
Giúp mik bài 4 vs mn, mik đag cần gấp



