Các câu hỏi tương tự
Một cái bồn gồm hai nửa hình cầu đường kính 18dm, và một hình trụ có chiều cao 36dm . Tính thể tích V của cái bồn đó.
Đọc tiếp
Một cái bồn gồm hai nửa hình cầu đường kính 18dm, và một hình trụ có chiều cao 36dm . Tính thể tích V của cái bồn đó.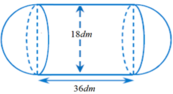

![]()
![]()
![]()
![]()
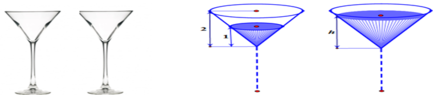
Hai chiếc ly đựng chất lỏng giống hệt nhau, mỗi chiếc có phần chứa chất lỏng là một khối nón có chiều cao 2 dm (mô tả như hình vẽ). Ban đầu chiếc ly thứ nhất chứa đầy chất lỏng, chiếc ly thứ hai để rỗng. Người ta chuyển chất lỏng từ ly thứ nhất sang ly thứ hai sao cho độ cao của cột chất lỏng trong ly thứ nhất còn 1dm. Tính chiều cao h của cột chất lỏng trong ly thứ hai sau khi chuyển (độ cao của cột chất lỏng tính từ đỉnh của khối nón đến mặt chất lỏng - lượng chất lỏng coi như không hao hụt kh...
Đọc tiếp
Hai chiếc ly đựng chất lỏng giống hệt nhau, mỗi chiếc có phần chứa chất lỏng là một khối nón có chiều cao 2 dm (mô tả như hình vẽ). Ban đầu chiếc ly thứ nhất chứa đầy chất lỏng, chiếc ly thứ hai để rỗng. Người ta chuyển chất lỏng từ ly thứ nhất sang ly thứ hai sao cho độ cao của cột chất lỏng trong ly thứ nhất còn 1dm. Tính chiều cao h của cột chất lỏng trong ly thứ hai sau khi chuyển (độ cao của cột chất lỏng tính từ đỉnh của khối nón đến mặt chất lỏng - lượng chất lỏng coi như không hao hụt khi chuyển. Tính gần đúng h với sai số không quá 0,01dm).
![]()
![]()
![]()
![]()
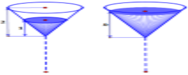
Hai chiếc ly đựng chất lỏng giống hệt nhau, mỗi chiếc có phần chứa chất lỏng là một khối nón có chiều cao 2 dm (mô tả như hình vẽ). Ban đầu chiếc ly thứ nhất chứa đầy chất lỏng, chiếc ly thứ hai để rỗng. Người ta chuyển chất lỏng từ ly thứ nhất sang ly thứ hai sao cho độ cao của cột chất lỏng trong ly thứ nhất còn 1dm. Tính chiều cao h của cột chất lỏng trong ly thứ hai sau khi chuyển (độ cao của cột chất lỏng tính từ đỉnh của khối nón đến mặt chất lỏng - lượng chất lỏng coi như không hao hụt kh...
Đọc tiếp
Hai chiếc ly đựng chất lỏng giống hệt nhau, mỗi chiếc có phần chứa chất lỏng là một khối nón có chiều cao 2 dm (mô tả như hình vẽ). Ban đầu chiếc ly thứ nhất chứa đầy chất lỏng, chiếc ly thứ hai để rỗng. Người ta chuyển chất lỏng từ ly thứ nhất sang ly thứ hai sao cho độ cao của cột chất lỏng trong ly thứ nhất còn 1dm. Tính chiều cao h của cột chất lỏng trong ly thứ hai sau khi chuyển (độ cao của cột chất lỏng tính từ đỉnh của khối nón đến mặt chất lỏng - lượng chất lỏng coi như không hao hụt khi chuyển. Tính gần đúng h với sai số không quá 0,01dm).

![]()
![]()
![]()
![]()
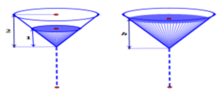
Hai chiếc ly đựng chất lỏng giống hệt nhau, mỗi chiếc có phần chứa chất lỏng là một khối nón có chiều cao 2 dm (mô tả như hình vẽ). Ban đầu chiếc ly thứ nhất chứa đầy chất lỏng, chiếc ly thứ hai để rỗng. Người ta chuyển chất lỏng từ ly thứ nhất sang ly thứ hai sao cho độ cao của cột chất lỏng trong ly thứ nhất còn 1dm. Tính chiều cao h của cột chất lỏng trong ly thứ hai sau khi chuyển (độ cao của cột chất lỏng tính từ đỉnh của khối nón đến mặt chất lỏng - lượng chất lỏng coi như không hao hụt kh...
Đọc tiếp
Hai chiếc ly đựng chất lỏng giống hệt nhau, mỗi chiếc có phần chứa chất lỏng là một khối nón có chiều cao 2 dm (mô tả như hình vẽ). Ban đầu chiếc ly thứ nhất chứa đầy chất lỏng, chiếc ly thứ hai để rỗng. Người ta chuyển chất lỏng từ ly thứ nhất sang ly thứ hai sao cho độ cao của cột chất lỏng trong ly thứ nhất còn 1dm. Tính chiều cao h của cột chất lỏng trong ly thứ hai sau khi chuyển (độ cao của cột chất lỏng tính từ đỉnh của khối nón đến mặt chất lỏng - lượng chất lỏng coi như không hao hụt khi chuyển. Tính gần đúng h với sai số không quá 0,01dm)

![]()
![]()
![]()
![]()
Viết công thức tính thể tích V của vật thể nằm giữa hai mặt phẳng x 0 và x ln4 bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x có thiết diện là một hình vuông có độ dài cạnh là
x
.
e
x
Đọc tiếp
Viết công thức tính thể tích V của vật thể nằm giữa hai mặt phẳng x = 0 và x = ln4 bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x có thiết diện là một hình vuông có độ dài cạnh là x . e x
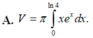
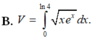
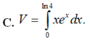
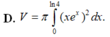
Một cái ống hình trụ tròn xoay bên trong rỗng, có chiều cao bằng 25cm và đường kính đáy bằng 6cm đặt trên cái bàn nằm ngang có mặt bàn phẳng sao cho một miệng ống nằm trên mặt bàn. Người ta đặt lên trên miệng ống còn lại một quả bóng hình cầu có bán kính 5cm. Tính khoảng cách lớn nhất h có thể từ một điểm trên quả bóng tới mặt bàn nếu coi độ dày của thành ống là không đáng kể.
Đọc tiếp
Một cái ống hình trụ tròn xoay bên trong rỗng, có chiều cao bằng 25cm và đường kính đáy bằng 6cm đặt trên cái bàn nằm ngang có mặt bàn phẳng sao cho một miệng ống nằm trên mặt bàn. Người ta đặt lên trên miệng ống còn lại một quả bóng hình cầu có bán kính 5cm. Tính khoảng cách lớn nhất h có thể từ một điểm trên quả bóng tới mặt bàn nếu coi độ dày của thành ống là không đáng kể.
![]()
![]()
![]()
![]()
Một cái bồn chứa nước gồm hai nửa hình cầu và một hình trụ (như hình vẽ). Đường sinh của hình trụ bằng hai lần đường kính của hình cầu. Biết thể tích của bồn chứa nước là
128
π
3
(
m
3
)
. Tính diện tích xung quanh của cái bồn chứa nước theo đơn vị
m
2
Đọc tiếp
Một cái bồn chứa nước gồm hai nửa hình cầu và một hình trụ (như hình vẽ). Đường sinh của hình trụ bằng hai lần đường kính của hình cầu. Biết thể tích của bồn chứa nước là 128 π 3 ( m 3 ) . Tính diện tích xung quanh của cái bồn chứa nước theo đơn vị m 2

![]()
![]()
![]()
![]()
Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ một góc 45°. Tính thể tích của khối trụ. A.
πa
3
2
16
B.
πa
3...
Đọc tiếp
Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ một góc 45°. Tính thể tích của khối trụ.
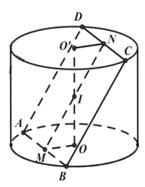
A. πa 3 2 16
B. πa 3 2 4
C. πa 3 2 2
D. 3 πa 3 2 16
Cho mặt nón có chiều cao h 6 bán kính đáy r 3. Một hình lập phương đặt trong mặt nón sao cho trục của mặt nón đi qua tâm hai đáy của hình lập phương, một đáy của hình lập phương nằm trong mặt đáy của hình nón, các đỉnh còn lại thuộc các đường sinh của hình nón. Tính độ dài cạnh của hình lập phương.
Đọc tiếp
Cho mặt nón có chiều cao h = 6 bán kính đáy r = 3. Một hình lập phương đặt trong mặt nón sao cho trục của mặt nón đi qua tâm hai đáy của hình lập phương, một đáy của hình lập phương nằm trong mặt đáy của hình nón, các đỉnh còn lại thuộc các đường sinh của hình nón. Tính độ dài cạnh của hình lập phương.
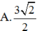
![]()
![]()
![]()


