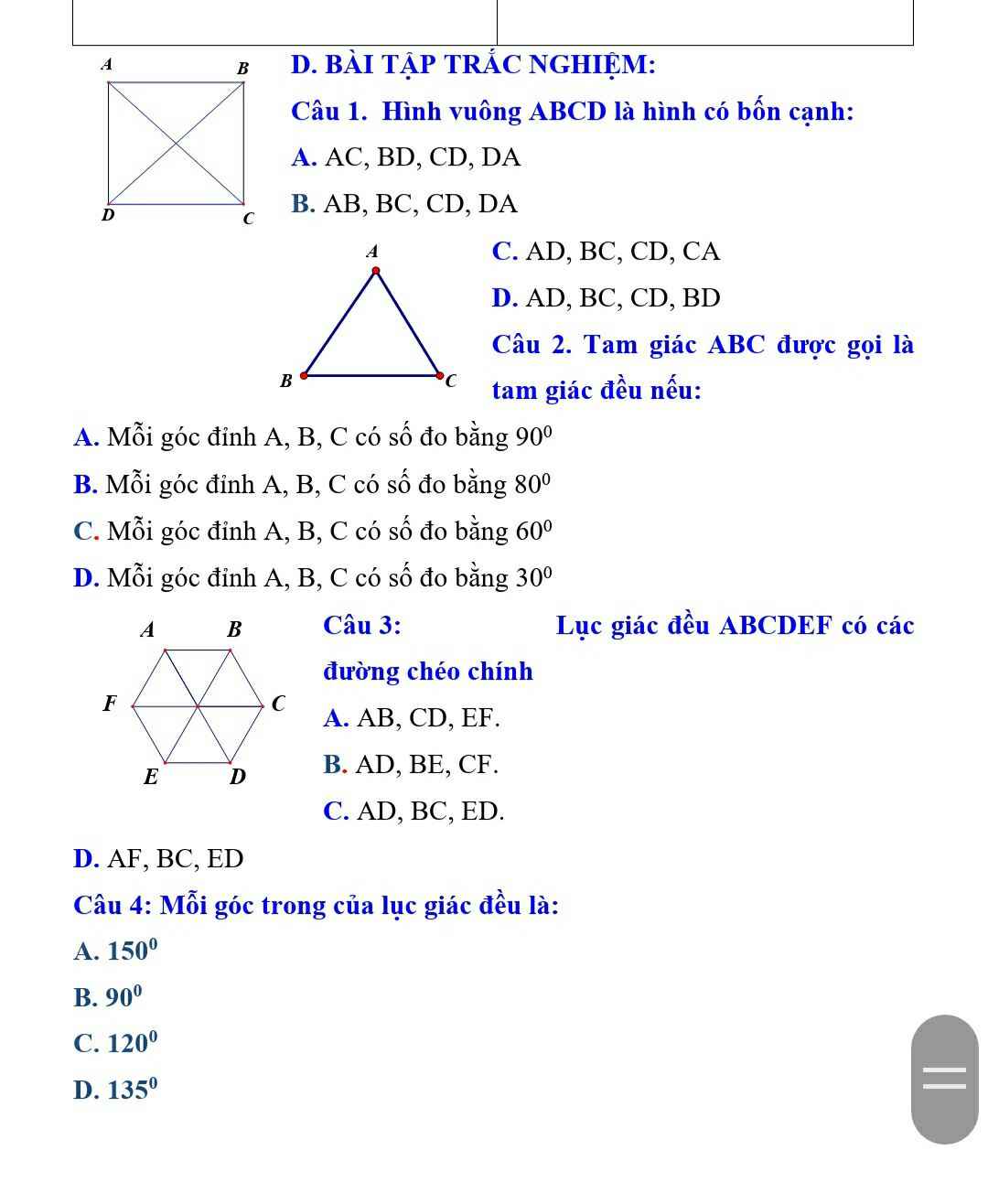
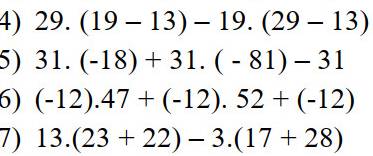=>\(\left(x-20\right)\cdot\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{200}}{\left(1+\dfrac{1}{199}\right)+\left(1+\dfrac{1}{198}\right)+...+\left(1+\dfrac{198}{2}\right)+1}=\dfrac{1}{2000}\)
=>(x-20)*1/200=1/2000
=>x-20=1/10
=>x=20,1
\(\left(x-20\right).\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{200}}{\dfrac{1}{199}+\dfrac{2}{198}+\dfrac{3}{197}+...+\dfrac{198}{2}+\dfrac{199}{1}}=\dfrac{1}{200}.\\ \left(x-20\right)\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{200}}{\left(1+\dfrac{1}{199}\right)+\left(1+\dfrac{2}{198}\right)+\left(1+\dfrac{3}{197}\right)+...+\left(1+\dfrac{198}{2}\right)+1}=\dfrac{1}{200}.\)
\(\left(x-20\right).\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{200}}{\dfrac{200}{199}+\dfrac{200}{198}+\dfrac{200}{197}+...+\dfrac{200}{2}+\dfrac{200}{200}}=\dfrac{1}{200}.\\ \left(x-20\right).\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{200}}{200\left(\dfrac{1}{199}+\dfrac{1}{198}+\dfrac{1}{197}+...+\dfrac{1}{2}+\dfrac{1}{200}\right)}=\dfrac{1}{200}.\\ \left(x-20\right).\dfrac{1}{200}=\dfrac{1}{200}.\)
\(\Rightarrow x-20=\dfrac{1}{200}:\dfrac{1}{200}=1.\\ \Rightarrow x=1+20=21.\)
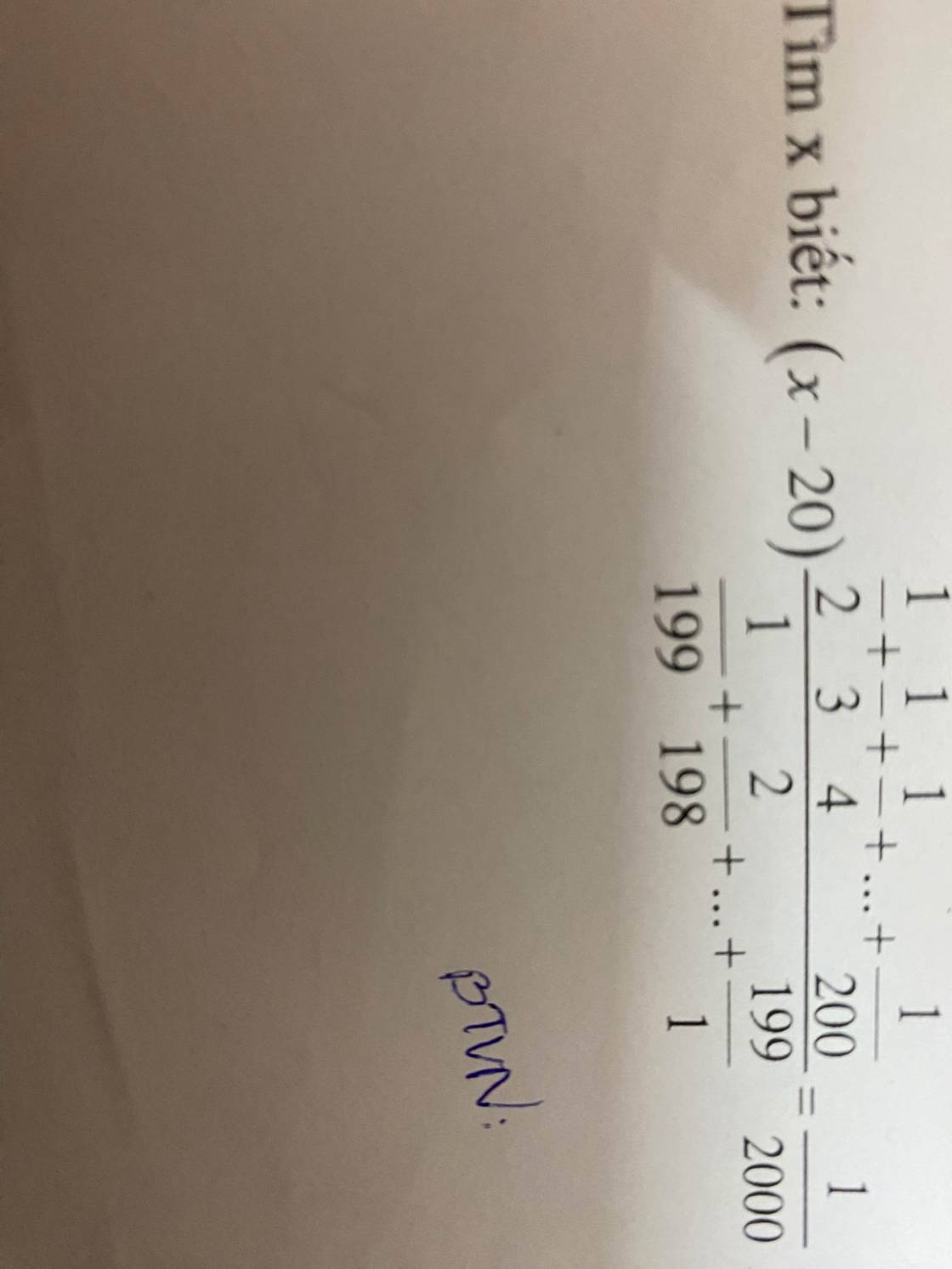
cứu cứu xong tui tăng sp cho
