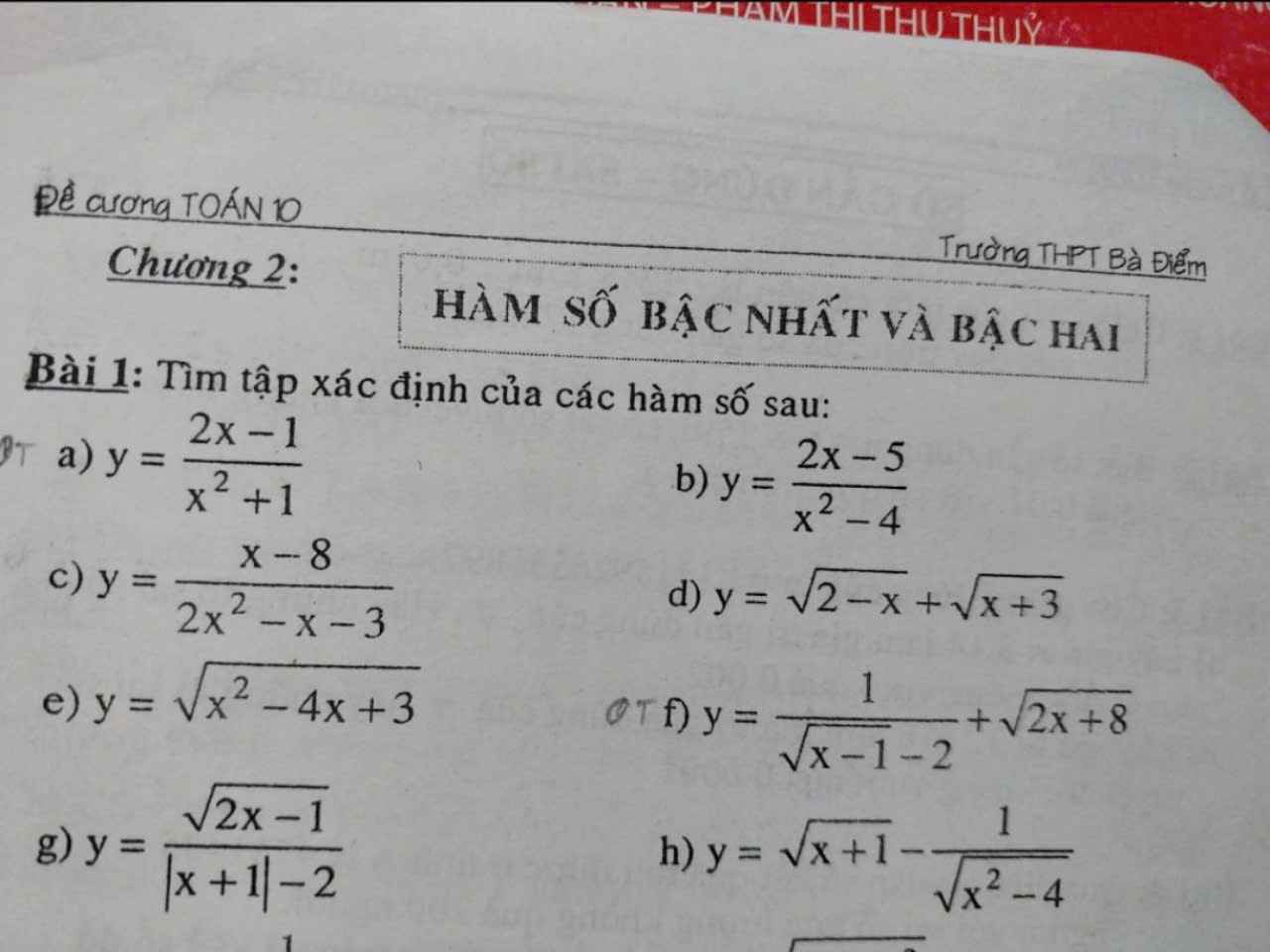a: ĐKXĐ: \(x^2+1\ne0\)
=>\(x^2\ne-1\)(luôn đúng)
Vậy: TXĐ là D=R
b: ĐKXĐ: \(x^2-4\ne0\)
=>\(x^2\ne4\)
=>\(x\notin\left\{2;-2\right\}\)
Vậy: TXĐ là D=R\{2;-2}
c: ĐKXĐ: \(2x^2-x-3\ne0\)
=>(2x-3)(x+1)\(\ne\)0
=>\(x\notin\left\{\dfrac{3}{2};-1\right\}\)
Vậy: Tập xác định là \(D=R\backslash\left\{\dfrac{3}{2};-1\right\}\)
d: ĐKXĐ: \(\left\{{}\begin{matrix}2-x>=0\\x+3>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =2\\x>=-3\end{matrix}\right.\)
=>-3<=x<=2
Vậy: TXĐ là D=[-3;2]
e: ĐKXĐ: \(x^2-4x+3>=0\)
=>(x-1)(x-3)>=0
=>\(\left[{}\begin{matrix}x>=3\\x< =1\end{matrix}\right.\)
Vậy: TXĐ là D=[3;+\(\infty\))\(\cup\)(-\(\infty\);1]
f: ĐKXĐ: \(\left\{{}\begin{matrix}x-1>=0\\\sqrt{x-1}-2\ne0\\2x+8>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>1\\x-1\ne4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>1\\x\ne5\end{matrix}\right.\)
vậy: TXĐ là \(D=\left(1;+\infty\right)\backslash\left\{5\right\}\)
g: ĐKXĐ: \(\left\{{}\begin{matrix}2x-1>=0\\\left|x+1\right|-2\ne0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{1}{2}\\x+1\notin\left\{2;-2\right\}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{1}{2}\\x\in\left\{-1;-3\right\}\end{matrix}\right.\Leftrightarrow x>=\dfrac{1}{2}\)
Vậy: TXĐ là \(D=[\dfrac{1}{2};+\infty)\)
h: ĐKXĐ: \(\left\{{}\begin{matrix}x+1>=0\\x^2-4>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-1\\x^2>4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-1\\\left[{}\begin{matrix}x>2\\x< -2\end{matrix}\right.\end{matrix}\right.\Leftrightarrow x>2\)
Vậy: TXĐ là \(D=\left(2;+\infty\right)\)