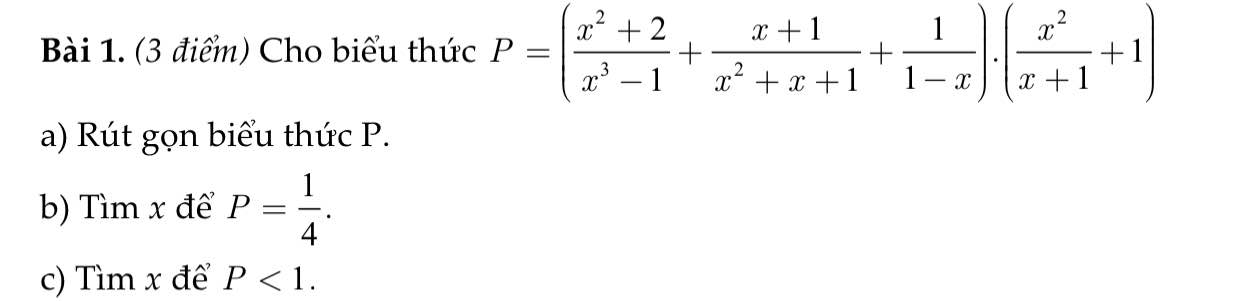Bài 3
1, \(A=-x^2+4x+1=-\left(x^2-4x+4-4\right)+1=-\left(x-2\right)^2+5\le5\)
Dấu ''='' xảy ra khi x = 2
2, \(B=-x^2-4x+3=-\left(x^2+4x+4-4\right)+3=-\left(x+2\right)^2+7\le7\)
Dấu ''='' xảy ra khi x = -2
3, \(C=-x^2-5x+8=-\left(x^2+5x+\dfrac{25}{4}-\dfrac{25}{4}\right)+8=-\left(x-\dfrac{5}{4}\right)^2+\dfrac{57}{4}\le\dfrac{57}{4}\)
Dấu ''='' xảy ra khi x = 5/4
4, \(D=-x^2+6x-4=-\left(x^2-6x+9-9\right)-4=-\left(x-3\right)^2+5\le5\)
Dấu ''='' xảy ra khi x = 3
5, \(E=-x^2-6x-10=-\left(x^2+6x+9-9\right)-10=-\left(x+3\right)^2-1\le-1\)
Dấu ''='' xảy ra khi x = -3
6, \(F=-x^2+13x+1=-\left(x^2-13x+\dfrac{13^2}{4}-\dfrac{13^2}{4}\right)+1=-\left(x-\dfrac{13}{2}\right)^2+\dfrac{173}{4}\le\dfrac{173}{4}\)
Dấu ''='' xảy ra khi x = 13/2
Bài 1:
1: \(A=x^2-x+1\)
\(=x^2-x+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}>0\forall x\)
2: \(B=x^2+x+1\)
\(=x^2+x+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}>0\forall x\)
3: \(C=x^2+2x+2\)
\(=x^2+2x+1+1\)
\(=\left(x+1\right)^2+1>=1>0\forall x\)
4: \(A=x^2-5x+10\)
\(=x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}+\dfrac{15}{4}\)
\(=\left(x-\dfrac{5}{2}\right)^2+\dfrac{15}{4}>=\dfrac{15}{4}>0\forall x\)
5: \(B=x^2-8x+20\)
\(=x^2-8x+16+4\)
\(=\left(x-4\right)^2+4>=4>0\forall x\)
6: \(C=x^2-8x+17\)
\(=x^2-8x+16+1\)
\(=\left(x-4\right)^2+1>=1>0\forall x\)
7: \(A=x^2-6x+10\)
\(=x^2-6x+9+1\)
\(=\left(x-3\right)^2+1>=1>0\forall x\)
8: \(B=9x^2-6x+2\)
\(=9x^2-6x+1+1\)
\(=\left(3x-1\right)^2+1>=1>0\forall x\)
9: \(C=2x^2+8x+15\)
\(=2x^2+8x+8+7\)
\(=2\left(x^2+4x+4\right)+7=2\left(x+2\right)^2+7>=7>0\forall x\)
giúp mình bài 3 vs mn ơi ko phải thi chỉ là đề ôn thôi ạ
