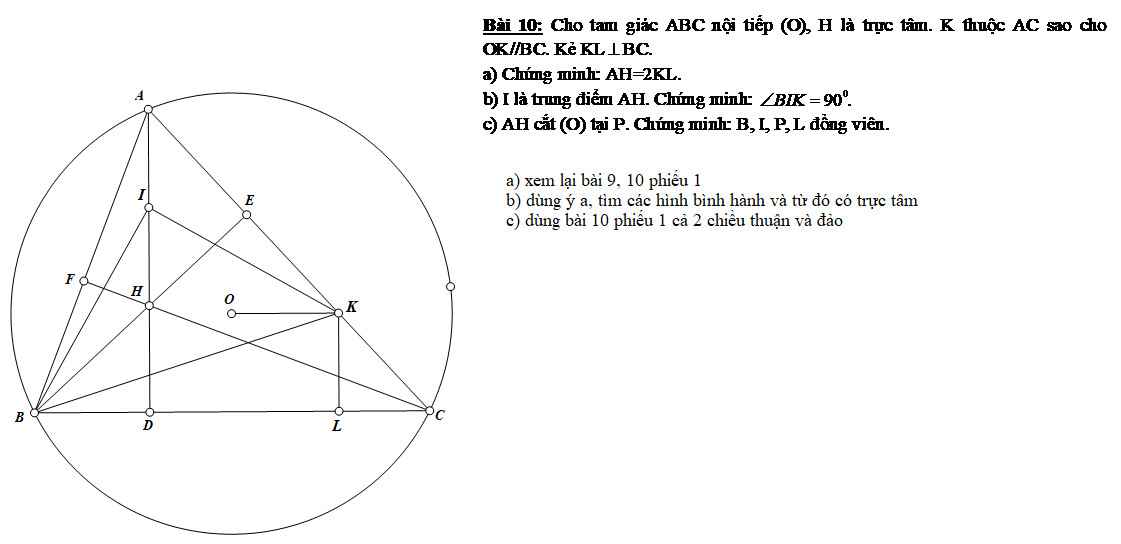
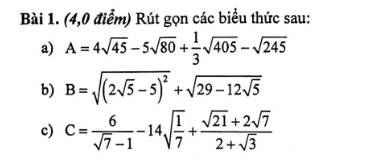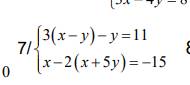\(a,\) Ta có :
\(OB=OC=R\)
\(AB=AC\) (t/c 2 tiếp tuyến cắt nhau)
\(\Rightarrow OA\) là đường trung trực của \(BC\)
\(\Rightarrow OA\perp BC\)
\(b,\) Xét \(\Delta ABE\) và \(\Delta ABD\) có :
\(\widehat{BAE}\) chung
\(\widehat{BED}=\widehat{ABD}\) (cùng chắn \(\stackrel\frown{BD}\) )
\(\Rightarrow\Delta ABE\sim\Delta ABD\left(g-g\right)\)
\(\Rightarrow\dfrac{AB}{AD}=\dfrac{AE}{AB}\)
\(\Rightarrow AB^2=AD.AE\)
Xét \(\Delta OAB\perp\) tại \(A\) có :
\(AB^2=AH.AO\left(HTL\right)\) \(\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\Rightarrow\) \(AD.AE=AH.AO\)
Xét \(\Delta AHD\) và \(\Delta AEO\) có :
\(\widehat{OAE}chung\)
\(\dfrac{AD}{AH}=\dfrac{AO}{AE}\left(AD.AE=AH.AO\right)\)
\(\Rightarrow\Delta AHD\sim\Delta AEO\left(c-g-c\right)\)
\(\Rightarrow\widehat{AHD}=\widehat{AEO}\)
\(\Rightarrow\) Tứ giác \(DHOE\) nội tiếp (góc ngoài = góc đối trong)