Chọn A.
Phương pháp:
Giải phương trình bằng phương pháp xét hàm số.
Cách giải:
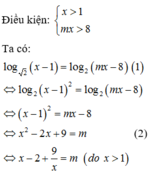
Phương trình (1) có 2 nghiệm thực phân biệt Û Phương trình (2) có 2 nghiệm thực phân biệt lớn hơn 1 (*)
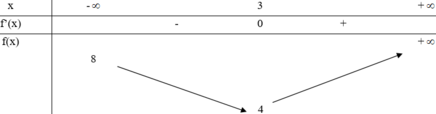
Xét hàm số
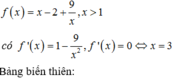
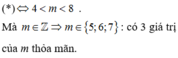
Chọn A.
Phương pháp:
Giải phương trình bằng phương pháp xét hàm số.
Cách giải:
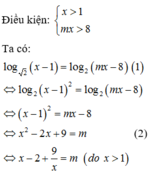
Phương trình (1) có 2 nghiệm thực phân biệt Û Phương trình (2) có 2 nghiệm thực phân biệt lớn hơn 1 (*)
Xét hàm số
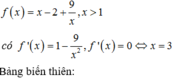

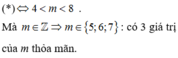
Có tất cả bao nhiêu số nguyên m để phương trình log ( m - x ) = 3 log ( 4 - 2 x - 3 ) có hai nghiệm thực phân biệt.
A. 6.
B. 2.
C. 3.
D. 5.
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình log ( ( m - 1 ) . 16 x + 2 . 25 x 5 . 20 x ) - 5 x + 1 . 4 x = ( 1 - m ) 4 2 x - 2 . 25 x có hai nghiệm thực phân biệt. Số phần tử của S bằng
A. 4.
B. 3.
C. 1.
D. 2.
Có tất cả bao nhiêu giá trị nguyên hàm của tham số m để phương trình 4 x 2 - 3 . 2 x 2 + 1 + m - 3 = 0 có 4 nghiệm phân biệt.
A. 3
B. 9
C. 12
D. 4
Có bao nhiêu giá trị nguyên của tham số m để phương trình log 2 4 x - m = x + 1 có đúng hai nghiệm phân biệt?
A. 0
B. 3
C. 1
D. 2
Có bao nhiêu giá trị nguyên của tham số m để phương trình ( m - 5 ) 9 x + ( 2 m - 2 ) 6 x + ( 1 - m ) 4 x = 0 có hai nghiệm phân biệt?
A. 2
B. 4
C. 3
D. 1
Cho phương trình m ln 2 x + 1 - x + 2 - m ln x + 1 - x - 2 = 0 1 . Tập tất cả giá trị của tham số m để phương trình 1 có các nghiệm, trong đó có hai nghiệm phân biệt thỏa mãn 0 < x 1 < 2 < 4 < x 2 là khoảng a ; + ∞ . Khi đó, a thuộc khoảng
A. (3,8;3,9)
B. (3,7;3,8)
C. (3,6;3,7)
D. (3,5;3,6)
Tìm tất cả các giá trị của tham số m để phương trình x - 2 log 3 x + 1 = m có hai nghiệm phân biệt.
A. -1 < m ≠ 0
B. m > -1
C. Không tồn tại m.
D. -1 < m < 0.
Tập tất cả các giá trị của tham số m để phương trình m 1 + x + 1 - x + 3 + 2 1 - x 2 - 5 = 0 có đúng hai nghiệm thức phân biệt là một nửa khoảng (a;b] . Tính b - 5 7 a
A. 6 - 5 2 7
B. 6 - 5 2 35
C. 12 - 5 2 25
D. 12 - 5 2 7
Tập tất cả các giá trị của tham số thực m để phương trình m 1 + x + 1 - x + 3 + 2 1 - x 2 - 5 = 0 có đúng hai nghiệm phân biệt là một nửa khoảng (a;b]. Tính b - 5 7 a
A. 6 - 5 2 35
B. 6 - 5 2 7
C. 12 - 5 2 35
D. 12 - 5 2 7