Chọn D
Số cách chọn 3 trong n học sinh có 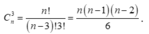
Khi đó ![]()
Chọn D
Số cách chọn 3 trong n học sinh có 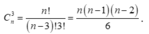
Khi đó ![]()
Có tất cả 120 cách chọn 3 học sinh từ nhóm n (chưa biết) học sinh. Số n là nghiệm của phương trình nào sau đây?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Đội dự tuyển học sinh giỏi Toán của tỉnh A có n học sinh n = 9 trong đó có 2 học sinh nữ, tham gia kì thi để chọn đội tuyển chính thức gồm 4 người. Biết xác suất trong đội tuyển chính thức cả 2 học sinh nữ gấp 2 lần xác suất trong đội tuyển chính thức không có học sinh nữ nào. Tìm n?
A. n = 9
B. n = 7
C. n = 5
D. n = 11
Một nhóm học sinh gồm 57 bạn được chia thành n (1<= n) nhóm, mỗi nhóm tối thiểu 5 học sinh. Tính số cách chia.
Chứng minh rằng:
a) Số các nghiệm tự nhiên của phương trình \(x_1+x_2+...+x_m=n\left(n,m\in N\cdot\right)\) là \(C^n_{m+n-1}\).
b) Số các nghiệm nguyên dương của phương trình \(x_1+x_2+...+x_m=n\left(m\le n;m,n\in N\cdot\right)\) là \(C^{m-1}_{n-1}\).
Em có tìm một số lời giải cho bài toán này nhưng vẫn không hiểu lắm, mong ai đó có lời giải chi tiết và dễ hiểu :)
Cho hàm số f(n)= a n + 1 + b n + 2 + c n + 3 ( n ∈ N * ) với a, b, c là hằng số thỏa mãn a+b+c=0. Khẳng định nào sau đây đúng?
A. lim x → + ∞ f ( n ) = - 1
B. lim x → + ∞ f ( n ) = 1
C. lim x → + ∞ f ( n ) = 0
D. lim x → + ∞ f ( n ) = 2
Một xe bus đưa p học sinh đi học về nhà sẽ đỗ ở n trạm( mỗi trạm học sinh có thể xuống từ 0 đến p học sinh). Hỏi có bao nhiêu cách để học sinh xuống xe hết? Đáp án là n+p-1C p-1, nhưng mình không biết cách giải giúp mình với
Cho dãy số (un) có un = 1/n+2 với n thuộc N*. Khẳng định nào sau đây là đúng?
Cho hàm số f(n)= 1+3+6+10+...+ n ( n + 1 ) 2 ( n ∈ N * ) .
Biết lim f ( n ) ( 3 n + 1 ) ( 5 n 2 + 2 ) = a b ( a , b ∈ Z ) phân số này tối giản. Giá trị b - 5a là
A.50
B.45
C.85
D.60
tìm tất cả các bộ (n,k,p), với n,k là các số nguyên lớn hơn 1 và p là 1 số nguyên tố thỏa mãn \(n^5+n^4-2n^3-2n^2+1=p^k\)