Lấy căn bậc 50 mỗi vế của bất phương trình ta nhận được
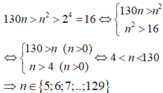
Từ đó có 125 số nguyên dương n thỏa mãn điều kiện đã cho
Chọn D
Lấy căn bậc 50 mỗi vế của bất phương trình ta nhận được
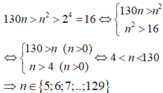
Từ đó có 125 số nguyên dương n thỏa mãn điều kiện đã cho
Chọn D
Cho f ( n ) = ( n 2 + n + 1 ) 2 ∀ n ∈ N * Đặt u n = f ( 1 ) . f ( 3 ) . . . f ( 2 n - 1 ) f ( 2 ) . f ( 4 ) . . . f ( 2 n ) .
Tìm số n nguyên dương nhỏ nhất sao cho u n thỏa mãn điều kiện log 2 u n + u n < - 10239 1024 .
A. n=23
B. n=29
C. n=21
D. n=33
Cho f ( n ) = ( n 2 + n + 1 ) 2 v ớ i ∀ n ∈ N * . Đặt u n = f ( 1 ) . f ( 3 ) . . . f ( 2 n - 1 ) f ( 2 ) . f ( 4 ) . . . f ( 2 n ) .
Tìm số n nguyên dương nhỏ nhất sao cho u n , thỏa mãn điều kiện log 2 u n + u n < - 10239 1024 .
A. n = 23
B. n = 29
C. n = 21
D. n = 33
Tìm tập S tất cả các số nguyên dương n thỏa điều kiện ∫ 1 e ln n x d x < e - 2
![]()
![]()
![]()
![]()
Gọi x, y là các số thực dương thỏa mãn điều kiện log 9 x = log 6 y = log 4 ( x + y ) và x y = - a + b 2 , với a, b là hai số nguyên dương. Tính a.b.
![]()
![]()
![]()
![]()
Gọi x và y là các số thực dương thỏa mãn điều kiện log 9 x = log 6 y = log 4 ( x + y ) và x y = - a + b 2 với a, b là hai số nguyên dương. Tính T = a + b
A. T=6
B. T=4
C. T=11
D. T=8
Gọi x, y là các số thực dương thỏa mãn điều kiện log9 x = log6 x = log4 (x + y) và biết rằng x y = - a + b 2 với a, b là các số nguyên dương. Tính giá trị a + b.
A. a + b = 6
B. a + b = 11
C. a + b = 4
D. a + b = 8
Gọi S là tập hợp số nguyên dương k thỏa mãn điều kiện: ∫ 1 e ln k x d x < e - 2 . Số phần tử của tập S là
A. 2
B. 1
C. 3
D. 0
Có bao nhiêu số phức z thỏa mãn điều kiện z . z ¯ + z = 2 và z = 2
A. 2
B. 3
C. 1
D. 4
Có bao nhiêu số phức z thỏa mãn điều kiện z z ¯ + z = 2 và z = 2 ?
A. 4
B. 3
C. 2
D. 1