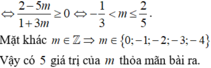Các câu hỏi tương tự
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
x
3
+
(
k
2
-
k
+
1
)
x
trên đoạn [-1;2]. Khi k thay đổi trên
ℝ
, giá trị nhỏ nhất c...
Đọc tiếp
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 3 + ( k 2 - k + 1 ) x trên đoạn [-1;2]. Khi k thay đổi trên ℝ , giá trị nhỏ nhất của M - m bằng.
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để hàm số liên tục và đạt giá trị nhỏ nhất trên [0;2] tại một điểm
x
0
∈
(
0
;
2
)
. A. m 1 B. -1 m 1 C. m 2 D. 0 m 1
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số 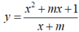 liên tục và đạt giá trị nhỏ nhất trên [0;2] tại một điểm
x
0
∈
(
0
;
2
)
.
liên tục và đạt giá trị nhỏ nhất trên [0;2] tại một điểm
x
0
∈
(
0
;
2
)
.
A. m > 1
B. -1 < m < 1
C. m > 2
D. 0 < m < 1
Tìm m để hàm số
f
(
x
)
m
x
+
5
x
-
m
đạt giá trị nhỏ nhất trên đoạn [0;1] bằng -7 A. m 2 B. m 1 C. m 0 D. m 5
Đọc tiếp
Tìm m để hàm số f ( x ) = m x + 5 x - m đạt giá trị nhỏ nhất trên đoạn [0;1] bằng -7
A. m = 2
B. m = 1
C. m = 0
D. m = 5
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
2
-
m
x
+
4
x
-
m
liên tục và đạt giá trị nhỏ nhất trên [0;4] tại một điểm ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 2 - m x + 4 x - m liên tục và đạt giá trị nhỏ nhất trên [0;4] tại một điểm x o ∈ ( 0 ; 4 ) .
A. m > 2
B. 0 < m < 2
C. -2<m<0
D. -2<m<2
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
2
+
m
x
+
1
x
+
m
liên tục và đạt giá trị nhỏ nhất trên [0;2] tại một điểm ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 2 + m x + 1 x + m liên tục và đạt giá trị nhỏ nhất trên [0;2] tại một điểm x o ∈ ( 0 ; 2 ) .
A. 0 < m <1
B. m > 1
C. m > 2
D. -1< m < 1
Kí hiệu a, b lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f (x) sin2x + 2sinx trên đoạn . Giá trị a +b bằng
Đọc tiếp
Kí hiệu a, b lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f (x) = sin2x + 2sinx trên đoạn  . Giá trị a +b bằng
. Giá trị a +b bằng
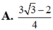
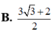
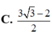
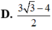
Kí hiệu a,b lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
f
x
sin
2
x
+
2
sin
x
trên đoạn
0
;
3
π
2
. Giá trị a+b bằng
Đọc tiếp
Kí hiệu a,b lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f x = sin 2 x + 2 sin x trên đoạn 0 ; 3 π 2 . Giá trị a+b bằng
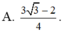
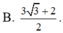
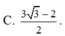

Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên Biểu thức có giá trị bằng: A. 0 B.
4
2
-
3
C. 2 D.
2
+
3
+
2
Đọc tiếp
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số ![]() trên Biểu thức có giá trị bằng:
trên Biểu thức có giá trị bằng:
A. 0
B. 4 2 - 3
C. 2
D. 2 + 3 + 2
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
-
1
+
2
.
cos
x
2
-
3
.
sin
x...
Đọc tiếp
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = - 1 + 2 . cos x 2 - 3 . sin x + cos x trên ℝ . Biểu thức M + N + 2 có giá trị bằng:
A. 0
B. 4 2 - 3
C. 2
D . 2 + 3 + 2
Hàm số f(x) 2.sinx + sin2x trên đoạn
0
,
3
π
2
có giá trị lớn nhất là M, giá trị nhỏ nhất là m. Khi đó M+m bằng:
A
.
-
3
3
B
.
3
3
C...
Đọc tiếp
Hàm số f(x) = 2.sinx + sin2x trên đoạn 0 , 3 π 2 có giá trị lớn nhất là M, giá trị nhỏ nhất là m. Khi đó M+m bằng:
A . - 3 3
B . 3 3
C . - 3 3 4
D . 3 3 2