Nối các đường chéo của các mặt ta được tứ diện đều không có đỉnh nào chung.
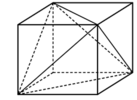
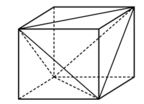
Mỗi tứ diện đều có tam giác đều. Nên tổng cộng có 8 tam giác đều. Chọn B.
Nối các đường chéo của các mặt ta được tứ diện đều không có đỉnh nào chung.


Mỗi tứ diện đều có tam giác đều. Nên tổng cộng có 8 tam giác đều. Chọn B.
Cho đa giác đều có 15 đỉnh. Gọi M là tập hợp các tam giác có ba đỉnh là ba đỉnh của đa giác đã cho. Chọn ngẫu nhiên một tam giác thuộc M, tính xác suất để tam giác được chọn là tam giác cân nhưng không phải là tam giác đều
A. 3/91
B. 18/91
C. 3/13
D. 1/26
Cho đa giác đều có 15 đỉnh. Gọi M là tập tất cả các tam giác có ba đỉnh là ba đỉnh của đa giác đã cho. Chọn ngẫu nhiên một tam giác thuộc tập M, tính xác suất để tam giác được chọn là một tam giác cân nhưng không phải là tam giác đều.
A. 73/91
B. 18/91
C. 8/91
D. 91/18
Một khối lập phương có độ dài cạnh là 2cm được chia thành 8 khối lập phương cạnh 1cm. Hỏi có bao nhiêu tam giác được tạo thành từ các đỉnh của khối lập phương cạnh 1cm
A. 2876
B. 2898
C. 2915
D. 2012
Một đa giác lồi có 10 đỉnh. Chọn ngẫu nhiên ba đỉnh của đa giác và nối chúng lại với nhau ta được một tam giác. Tính xác suất để tam giác thu được có ba cạnh là ba đường chéo của đa giác đã cho.
A. 11 12
B. 1 4
C. 3 8
D. 5 12
Cho đa giác đều 12 đỉnh. Gọi S là tập các hình tứ giác tạo từ 12 đỉnh trên. Chọn một phần tử từ tập S. Xác suất để tứ giác chọn được là hình chữ nhật.
A. 1 165
B. 1 33
C. 2 15
D. 4 195
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a, đỉnh A’ cách đều ba đỉnh A, B, C. Cạnh bên AA’ tạo với đáy một góc 45 ° Thể tích khối lăng trụ ABC.A’B’C’ bằng bao nhiêu?
A. a 3 10 10
B. a 3 3 12
C. a 3 4
D. a 3 8
Chọn ngẫu nhiên 3 đỉnh của một đa giác đều 20 đỉnh. Xác suất để chọn được 3 đỉnh lập thành một tam giác nhọn bằng
A. 6 19
B. 4 19
C. 3 19
D. 9 19
Chọn ngẫu nhiên 3 đỉnh của một đa giác đều 20 đỉnh. Xác suất để chọn được 3 đỉnh lập thành một tam giác nhọn bằng
A. 6 19
B. 4 19
C. 3 19
D. 9 19
Cho một đa giác đều có 18 đỉnh nội tiếp trong một đường tròn tâm O. Gọi X là tập các tam giác có các đỉnh là các đỉnh của đa giá trên. Tính xác suất để chọn được một tam giác từ tập X là tam giác cân nhưng không phải là tam giác đều.
A. 23 136
B. 144 136
C. 3 17
D. 7 816