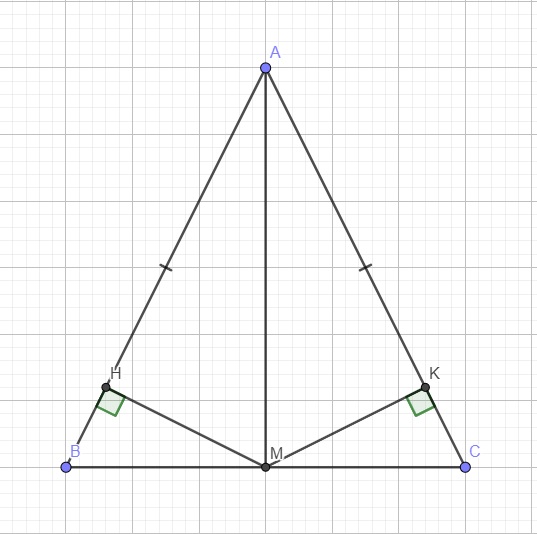
3.a
Do tam giác ABC cân tại A \(\Rightarrow\left\{{}\begin{matrix}AB=AC\\\widehat{B}=\widehat{C}\end{matrix}\right.\)
Do M là trung điểm BC \(\Rightarrow BM=CM\)
Xét hai tam giác ABM và tam giác ACM có:
\(\left\{{}\begin{matrix}AB=AC\left(cmt\right)\\\widehat{B}=\widehat{C}\left(cmt\right)\\BM=CM\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.g.c\right)\)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}\)
Mà \(\widehat{AMB}+\widehat{AMC}=180^0\)
\(\Rightarrow2.\widehat{AMB}=180^0\)
\(\Rightarrow\widehat{AMB}=90^0\)
\(\Rightarrow AM\perp BC\)
b.
Từ \(\Delta ABM=\Delta ACM\Rightarrow\widehat{MAB}=\widehat{MAC}\)
hay \(\widehat{MAH}=\widehat{MAK}\)
Do \(MH\perp AB\) và \(MK\perp AC\) nên \(\Delta AMH\) vuông tại H và \(\Delta AMK\) vuông tại K
Xét hai tam giác vuông AMH và AMK có:
\(\left\{{}\begin{matrix}AM\text{ là cạnh chung}\\\widehat{MAH}=\widehat{MAK}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta_{\perp}AMH=\Delta_{\perp}AMK\left(ch-gn\right)\)
\(\Rightarrow MH=MK\)