Đáp án C
Không gian mẫu Ω có số phần tử là n Ω = 10 ! .
Gọi A là biến cố “Xếp được dòng chữ “NƠI NÀO CÓ Ý CHÍ NƠI ĐÓ CÓ CON ĐƯỜNG”. Số phần tử của biến cố A là n A = 1 .
Vậy xác suất cần tính là P A = n A n Ω = 1 10 ! = 1 3628800 .
Đáp án C
Không gian mẫu Ω có số phần tử là n Ω = 10 ! .
Gọi A là biến cố “Xếp được dòng chữ “NƠI NÀO CÓ Ý CHÍ NƠI ĐÓ CÓ CON ĐƯỜNG”. Số phần tử của biến cố A là n A = 1 .
Vậy xác suất cần tính là P A = n A n Ω = 1 10 ! = 1 3628800 .
Có 10 tấm bìa ghi chữ “NƠI”, “NÀO”, “CÓ”, “Ý”, “CHÍ”, “NƠI”, “ĐÓ”, “CÓ”, “CON”, “ĐƯỜNG”. Một người phụ nữ xếp ngẫu nhiên 10 tấm bìa cạnh nhau. Tính xác suất để xếp các tấm bìa được dòng chữ “ NƠI NÀO CÓ Ý CHÍ NƠI ĐÓ CÓ CON ĐƯỜNG”.
A. 1 40320
B. 1 10
C. 1 3628800
D. 1 907200
Có 16 tấm bìa ghi 16 chữ “HỌC”, “ĐỂ”, “BIẾT”, “HỌC”, “ĐỂ”, “LÀM”, “HỌC”, “ĐỂ”, “CHUNG”, “SỐNG”, “HỌC”, “ĐỂ”, “TỰ”, “KHẲNG”, “ĐỊNH”, “MÌNH”. Một người xếp ngẫu nhiên 16 tấm bìa cạnh nhau. Tính xác suất để xếp các tấm bìa được dòng chữ “HỌC ĐỂ BIẾT HỌC ĐỂ LÀM HỌC ĐỂ CHUNG SỐNG HỌC ĐỂ TỰ KHẲNG ĐỊNH MÌNH”.
A. 8 16 !
B. 4 ! 16 !
C. 1 16 !
D. 4 ! . 4 ! 16 !
Trong một hộp có chứa các tấm bìa dạng hình chữ nhật có kích thước đôi một khác nhau, các cạnh của hình chữ nhật có kích thước là m và n ( m , n ∈ N ; 1 ≤ m , n ≤ 20 , đơn vị là cm). Biết rằng mỗi bộ kích thước ( m,n) đều có tấm bìa tương ứng. Ta gọi một tấm bìa là “tốt” nếu tấm bìa đó có thể được lắp ghép từ các miếng bìa dạng hình chữ L gồm 4 ô vuông, mỗi ô có độ dài cạnh là 1cm để tạo thành nó (Xem hình vẽ minh họa một tấm bìa “tốt” bên dưới) .
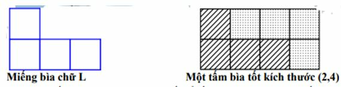
Rút ngẫu nhiên một tấm bìa từ hộp, tính xác suất để tấm bìa vừa rút được là tấm bìa “tốt”
A. 29/95
B. 2/7
C. 29/105
D. 9/35
An và Bình chơi một trò chơi. An để một sấp tấm bìa cứng nhỏ trên có ghi tương ứng các số từ 1 đến 30. Luật chơi như sau: Khi đến lượt, người chơi sẽ rút ngẫu nhiên 3 tấm bìa trong sấp và tính tổng các số ghi trên mỗi tấm bìa, trò chơi kết thúc khi có người thắng là người rút trúng 3 tấm bìa trên đó tổng các số chia hết cho 3. Lưu ý rằng không được để lại các tấm bìa đã rút vào sấp bài. Nếu Bình bốc trước, xác suất để Bình thắng ngay trong lượt đầu là:
A. 68 203
B. 77 203
C. 145 203
D. 119 203
An và Bình chơi một trò chơi. An để một sấp tấm bìa cứng nhỏ trên có ghi tương ứng các số từ 1 đến 30. Luật chơi như sau: Khi đến lượt, người chơi sẽ rút ngẫu nhiên 3 tấm bìa trong sấp và tính tổng các số ghi trên mỗi tấm bìa, trò chơi kết thúc khi có người thắng là người rút trúng 3 tấm bìa trên đó tổng các số chia hết cho 3. Lưu ý rằng không được để lại các tấm bìa đã rút vào sấp bài. Nếu Bình bốc trước, xác suất để Bình thắng ngay trong lượt đầu là:
A. 68 203
B. 77 203
C. 145 203
D. 119 203
Có thể dùng 3 tấm bìa hình tròn đường kính 1 dm để che kín 1 tấm bìa hình vuông cạnh 1 dm không? ( các tấm bìa có thể chồng lên nhau)
Có thể dùng 3 tấm bìa hình vuông cạnh 4 dm để che kín 1 tấm bìa hình vuông cạnh 5 dm không? ( các tấm bìa có thể chồng lên nhau)
Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một hình vuông cạnh 12cm rồi gấp lại thành một hình hộp chữ nhật không có nắp. Khi dung tích của cái hộp đó là 4800 c m 3 , tính độ dài cạnh của tấm bìa
A. 42 cm
B. 36 cm
C. 44 cm
D. 38 cm
Có 10 tấm thẻ được đánh số từ 1 đến 30. Chọn ngẫu nhiên ra 10 tấm thẻ. Tính xác suất để trong 10 tấm thẻ có 5 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn và có đúng một tấm thẻ mang số chia hết cho 10.
A. 99 667
B. 634 667
C. 33 667
D. 568 667
Thầy Bình đặt lên bàn 30 tấm thẻ đánh số từ 1 đến 30. Bạn An chọn ngẫu nhiên 10 tấm thẻ. Tính xác suất để trong 10 tấm thẻ lấy ra có 5 tấm thẻ mang số lẻ và 5 tấm thẻ mang số chẵn, trong đó chỉ có một tấm mang số chia hết cho 10.
A. 99/66 7
B. 8/11
C. 3/11
D. 99/167