1. Để p/s tối giản thì tử và mẫu phải nguyên tố cùng nhau.
Gọi $d=ƯCLN(3n+5, n+7)$
$\Rightarrow 3n+5\vdots d; n+7\vdots d$
$\Rightarrow 3(n+7)-(3n+5)\vdots d$
$\Rightarrow 16\vdots d$
Vì $16=2^4$ nên để $3n+5, n+7$ nguyên tố cùng nhau thì $n+7\not\vdots 2$
$\Rightarrow n+7$ lẻ
$\Rightarrow n$ chẵn
Vậy với mọi $n$ chẵn thì ps tối giản.
2.
1. Để p/s tối giản thì tử và mẫu phải nguyên tố cùng nhau.
Gọi $d=ƯCLN(5n+7, 2n+1)$
$\Rightarrow 5n+7\vdots d; 2n+1\vdots d$
$\Rightarrow 2(5n+7)-5(2n+1)\vdots d$
$\Rightarrow 9\vdots d$
Vì $9=3^2$ nên để $5n+7, 2n+1$ nguyên tố cùng nhau thì $2n+1\not\vdots 3$
$\Rightarrow 2n-2\not\vdots 3$
$\Rightarrow 2(n-1)\not\vdots 3$
$\Rightarrow n-1\not\vdots 3$
$\Rightarrow n\neq 3k+1$ với mọi $k$ tự nhiên bất kỳ.
3. Để ps tối giản thì tử và mẫu nguyên tố cùng nhau
Gọi $d=ƯCLN(5-2n, 4n+5)$
$\Rightarrow 5-2n\vdots d; 4n+5\vdots d$
$\Rightarrow 2(5-2n)+(4n+5)\vdots d$
$\Rightarrow 15\vdots d$
Vì $15=3.5$ nên để ps tối giản thì $d=1$, tức là $d\neq 3,5,15$.
Điều này xảy ra khi $5-2n\not\vdots 3$ và $5-2n\not\vdots 5$
$5-2n\not\vdots 3$
$\Rightarrow 2-2n\not\vdots 3$
$\Rightarrow 2n-2\not\vdots 3\Rightarrow 2(n-1)\not\vdots 3$
$\Rightarrow n-1\not\vdots 3\Rightarrow n=3k+2$ hoặc $n=3k$ với mọi $k$ tự nhiên (1)
$5-2n\not\vdots 5$
$\Rightarrow 2n\not\vdots 5$
$\Rightarrow n\not\vdots 5$ (2)
Từ $(1); (2)\Rightarrow n=15t+2, 15t+3, 15t+6, 15t+8, 15t+9, 15t+12, 15t+14$ với $t$ là số tự nhiên bất kỳ

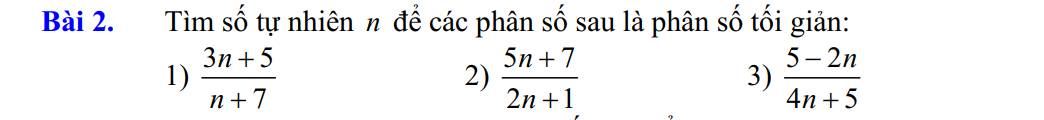






 Cíu mk với :
Cíu mk với :
 CÍU VỚI< GẤP
CÍU VỚI< GẤP



