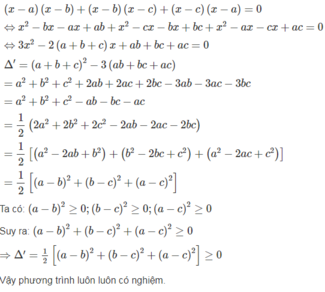Các câu hỏi tương tự
Cho phương trình x2+bx+c=0 (*) với b,c là các số thõa mãn 2b+4c=-1
a. chứng tỏ rằng phương trình (*) luôn có nghiệm
b. Tìm b,c biết rằng phương trình (*) có 2 nghiệm x1,x2 với x1-2x2=0
chứng minh rằng 3 số a,b,c là các số thực thì phương trình sau luôn có nghiệm:(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)=0
a) Chứng minh rằng với a, b , c là các số thực thì phương trình sau luôn có nghiệm:(x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a) 0b) Chứng minh rằng với ba số thức a, b , c phân biệt thì phương trình sau có hai nghiệm phân biết: c) Chứng minh rằng phương trình: c2x2 + (a2 – b2 – c2)x + b2 0 vô nghiệm với a, b, c là độ dài ba cạnh của một tam giác.d) Chứng minh rằng phương trình bậc hai:(a + b)2x2 – (a – b)(a2 – b2)x – 2ab(a2 + b2) 0 luôn có hai nghiệm phân biệt.
Đọc tiếp
a) Chứng minh rằng với a, b , c là các số thực thì phương trình sau luôn có nghiệm:
(x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a) = 0
b) Chứng minh rằng với ba số thức a, b , c phân biệt thì phương trình sau có hai nghiệm phân biết: 
c) Chứng minh rằng phương trình: c2x2 + (a2 – b2 – c2)x + b2 = 0 vô nghiệm với a, b, c là độ dài ba cạnh của một tam giác.
d) Chứng minh rằng phương trình bậc hai:
(a + b)2x2 – (a – b)(a2 – b2)x – 2ab(a2 + b2) = 0 luôn có hai nghiệm phân biệt.
Cho phương trình : x² - 2( m-1)x - 2m=0(I) a. Chứng tỏ rằng phương trình (I) luôn có hai nghiệm phân biệt với mọi giá trị m b. Tính X1 + X2 ; X1.X, theo m c. Tìm m để x1² + x2² = 4
C/tỏ rằng các phương trình sau luôn có nghiệm với mọi a, b:
\(x\left(x-a\right)+x\left(x-b\right)+\left(x-a\right)\left(x-b\right)=0\)
Cho phương trình: x2 – 2(2m + 1)x + 2m – 4 = 0.
a) Giải phương trình khi m = 1 và chứng tỏ tích hai nghiệm của phương trình luôn nhỏ hơn 1.
b) Có giá trị nào của m để phương trình có nghiệm kép không?
c) Gọi x1, x2 là hai nghiệm của phương trình, chứng minh rằng biểu thức: M = x1(1 – x2) + x2(1 – x1) là một hằng số.
với a,b,c là các số thực chứng minh phương trình sau luôn có nghiệm
(x-a)(x-b) + (x-b)(x-c) + (x-c)(x-a) = 0
C/tỏ rằng các phương trình sau luôn có nghiệm với mọi a, b:
\(x^2+\left(a+b\right)x-2\left(a^2-a+b^2\right)=0\)
Cho phương trình : x - 2( m-1)x - 2m=0 (I) a. Chúng tỏ rằng phương trình (I) luôn có hai nghiệm phân biệt với mọi giá trị m b. Tính Xi + X ; XI.X, theo m c. Tìm m để 2 X1² + x2² = 4