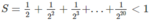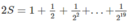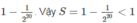9 tháng 5 2022 lúc 18:46
Các câu hỏi tương tự
S = \(\dfrac{1}{1^2}\) +\(\dfrac{1}{2^2}\)+\(\dfrac{1}{3^2}\)+\(\dfrac{1}{4^2}\)+....+\(\dfrac{1}{50^2}\). Chứng minh rằng S < 2
Cho dfrac{1}{2^2}+dfrac{1}{3^2}+dfrac{1}{4^2}+...+dfrac{1}{20^2} Chứng minh rằng : A 1
Đọc tiếp
Cho \(\dfrac{1}{2^2}\)+\(\dfrac{1}{3^2}\)+\(\dfrac{1}{4^2}\)+...+\(\dfrac{1}{20^2}\)
Chứng minh rằng : A < 1
Cho \(S=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{10^2}.\) Chứng minh rằng: \(S>\dfrac{9}{22}\)
28 tháng 4 2022 lúc 12:32
a)chứng minh rằng :dfrac{1}{3^2}+dfrac{1}{4^2}+dfrac{1}{5^2}+dfrac{1}{6^2}........+dfrac{1}{100^2} dfrac{1}{2}b)tính nhanh tổng S với S dfrac{1}{3.5}+dfrac{1}{5.7}+dfrac{1}{7.9}+......+dfrac{1}{61.63}các cao nhân gải giúp với ạ !!! iem đang cần gấp
Đọc tiếp
a)chứng minh rằng :\(\dfrac{1}{3^2}\)+\(\dfrac{1}{4^2}\)+\(\dfrac{1}{5^2}\)+\(\dfrac{1}{6^2}\)........+\(\dfrac{1}{100^2}< \dfrac{1}{2}\)
b)tính nhanh tổng S với S= \(\dfrac{1}{3.5}+\dfrac{1}{5.7}+\dfrac{1}{7.9}+......+\dfrac{1}{61.63}\)
các cao nhân gải giúp với ạ !!! iem đang cần gấp
\(S=\dfrac{1}{2^2}+\dfrac{1}{4^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}\) Chứng minh rằng \(S< \dfrac{1}{2}\)
CHo S=\(\dfrac{1}{4}+\dfrac{2}{4^2}+\dfrac{3}{4^3}+\dfrac{4}{4^4}+...+\dfrac{2023}{4^{2023}}\). Chứng minh S < \(\dfrac{1}{2}\)
Cho biểu thức S=\(\dfrac{1}{1}+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{63}\)
Chứng minh rằng 3<S<6
Chứng minh S<\(\dfrac{5}{32}\)
Cho \(S=\dfrac{1}{5^2}+\dfrac{1}{7^2}+...+\dfrac{1}{103^2}\)
Bài 1:
a, Tính \(\dfrac{5.4^{15}.9^{9} - 4.3^{20}.8^{9}}{5.2^{9}.6^{19}-7.2^{29}.27^{6}}\)
b,Tìm x biết:
\(1\dfrac{1}{30}:(24\dfrac{1}{6}-24\dfrac{1}{5}) -\dfrac{1\dfrac{1}{2}-\dfrac{3}{4}}{4x-\dfrac{1}{2}}=(-1\dfrac{1}{15}):(8\dfrac{1}{5}-8\dfrac{1}{3})\)
Bài 2: Chứng minh số:
222...22200333...333(2001c/s 2; 2003 c/s3)