Các câu hỏi tương tự
cho tứ giac ABCD .Goij M và N lần lượt là trung điểm của AB và CD. lấy các điểm P ,Q lần lươt thuộc các đường thẳng AD và BC sao cho vec tơ PA 2 vec tơ PD, vec tơ QP 2 vec tơ QC. tính vec tơ MN giúp tui
Cho tam giác ABC và M là trung điểm BC. Phân tích vec tơ AM theo vec tơ BA và vec tơ CA
Cho hai vec tơ và {displaystyle {vec {d}}}đều khác Gọi là góc giữa hai vec tơ đó.Ta có
Đọc tiếp
Cho hai vec tơ ![]() và {\displaystyle {\vec {d}}}
và {\displaystyle {\vec {d}}}![]() đều khác
đều khác ![]() Gọi
Gọi ![]() là góc giữa hai vec tơ đó.
là góc giữa hai vec tơ đó.
Ta có ![]()
Trong mặt phẳng tọa độ, các mệnh đề sau đúng hay sai?a) a→ (-3; 0) và i→ (1; 0) là hai vec tơ ngược hướng.b) a→ (3; 4) và b→ (-3; -4) là hai vec tơ đối nhauc) a→ (5; 3) và b→ (3; 5) là hai vec tơ đối nhau.d) Hai vec tơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.
Đọc tiếp
Trong mặt phẳng tọa độ, các mệnh đề sau đúng hay sai?
a) a→ (-3; 0) và i→ (1; 0) là hai vec tơ ngược hướng.
b) a→ (3; 4) và b→ (-3; -4) là hai vec tơ đối nhau
c) a→ (5; 3) và b→ (3; 5) là hai vec tơ đối nhau.
d) Hai vec tơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.
Trên đường thẳng chứa cạnh BC của tam giác ABC lấy điểm M sao cho . Hãy phân tích vec tơ theo hai vec tơ
Đọc tiếp
Trên đường thẳng chứa cạnh BC của tam giác ABC lấy điểm M sao cho 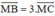 . Hãy phân tích vec tơ
. Hãy phân tích vec tơ 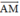 theo hai vec tơ
theo hai vec tơ 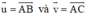
Bài 4. Cho tam giác ABC có AM là đường trung tuyến và D là trung điểm của AM. a) Chứng minh rằng: 2 vec DA + vec DB + vec DC = vec 0 b) Chứng minh rằng: vec BD = 1 2 vec B vec A + 1 4 vec BC . c) Gọi E là điểm trên cạnh AC sao cho AE = 1/3 * A * C Chứng minh rằng B, D, E thẳng hàng. Tính tỉ số (DB)/(DE)
Cho hai vec tơ a→ và b→ có
a
→
3
,
b
→
3
,
a
→
,
b
→
...
Đọc tiếp
Cho hai vec tơ a→ và b→ có a → = 3 , b → = 3 , a → , b → = 120 ° . Với giá trị nào của m thì hai vec tơ a → + m b → v à a → - m b → vuông góc với nhau?
Cho hình bình hành ABCD tâm O. Gọi M, N lần lượt là trung điểm của BC, CD; G là trọng tâm tam giác ABC.
a) Chứng minh AM + AN = 3/2 AC và GA +3GB+GC+GD=0
c) Gọi I là điểm thỏa mãn AI= 3/4AB. Phân tích IN ; IG theo hai vec tơ BA và BC
Chứng minh 3 điểm N;G;I thẳng hàng.
Lập phương trình tham số của đường thằng d trong mỗi trường hợp sau:a) d đi qua điểm M(2; 1) và có vec tơ chỉ phương ;b) d đi qua điểm M(–2; 3) và có vec tơ pháp tuyến
Đọc tiếp
Lập phương trình tham số của đường thằng d trong mỗi trường hợp sau:
a) d đi qua điểm M(2; 1) và có vec tơ chỉ phương 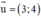 ;
;
b) d đi qua điểm M(–2; 3) và có vec tơ pháp tuyến 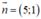
Cho 2 vec tơ
a
→
(
a
1
;
a
2
)
;
v
à
b
→
(
b
1
;
b
2
)
. Biểu thức sai là: A. B. C. D.
Đọc tiếp
Cho 2 vec tơ a → ( a 1 ; a 2 ) ; v à b → ( b 1 ; b 2 ) . Biểu thức sai là:
A. ![]()
B.![]()
C. 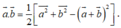
D.![]()







