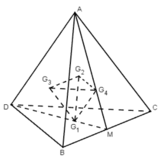
Xét tứ diện đều A.BCD cạnh bằng a. Gọi G 1 , G 2 , G 3 v à G 4 lần lượt là tâm của các tam giác BCD, ACD, ABD và ABC.
Gọi M là trung điểm của BC.
Xét tam giác AMD có:
Gọi O là tâm của một hình tứ diện đều. Từ một điểm M bất kì trên 1 mặt của tứ diện, ta hạ các đường vuông góc tới ba mặt còn lại. Giả sử K,L,N là chân các đường vuông góc nói trên. Chứng minh đường thẳng OM đi qua trọng tâm tam giác KLN
Khẳng đỉnh nào sau đây là sai?
A. Có một mặt cầu đi qua các đỉnh của một tứ diện bất kì.
B. Có một mặt cầu đi qua các đỉnh của một hình lăng trụ có đáy là một tứ giác lồi.
C. Có một mặt cầu đi qua các đỉnh của một hình hộp chữ nhật.
D. Có một mặt cầu đi qua các đỉnh của một hình chóp đều.
Cho tứ diện đều ABCD. Gọi (H) là hình bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện đều đó. Tính tỉ số: V H V ABCD
Chứng minh rằng tổng các khoảng cách từ một điểm bất kì trong một tứ diện đều đến các mặt phẳng của nó là một số không đổi.
Cho tứ diện đều ABCD cạnh a. Gọi H là hình chiếu vuông góc của đỉnh A xuống mặt phẳng (BCD).
Chứng minh H là tâm đường tròn ngoại tiếp tam giác BCD. Tính độ dài đoạn AH.
Các trung điểm của các cạnh của một tứ diện đều cạnh a là các đỉnh của khối đa diện đều. Tính thể tích V của khối đa diện đều đó.
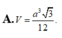
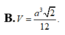
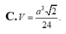
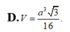
Một hình trụ có các đáy là hai hình tròn tâm O và O’ bán kính r và có đường cao h = r 2 . Gọi A là một điểm trên đường tròn tâm O và B là một điểm trên đường tròn tâm O’ sao cho OA vuông góc với O’B. Chứng minh rằng các mặt bên của tứ diện OABO’ là những tam giác vuông. Tính thể tích của tứ diện này.
Cho tứ diện đều ABCD cạnh 2a. Tính thể tích của khối bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện ABCD.
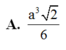
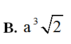
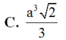
Chứng minh rằng nếu có một mặt cầu tiếp xúc với 6 cạnh của một hình tứ diện thì tổng các cặp cạnh đối diện của tứ diện bằng nhau.
