Các câu hỏi tương tự
Dựa vào công thức tính diện tích của đa giác đều để chứng minh công thức tính diện tích hình tròn
Một hình phẳng được giới hạn bởi y
e
-
x
, y 0, x 0, x 1. Ta chia đoạn [0; 1] thành n phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật con như Hình bên).a) Tính diện tích Sn của hình bậc thang (tổng diện tích của n hình chữ nhật con).b) Tìm và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân.
Đọc tiếp
Một hình phẳng được giới hạn bởi y = e - x , y = 0, x = 0, x = 1. Ta chia đoạn [0; 1] thành n phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật con như Hình bên).
a) Tính diện tích Sn của hình bậc thang (tổng diện tích của n hình chữ nhật con).
b) Tìm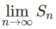 
và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân.
Tính tổng A=12 + 22 + 32 + 42 + ... + N2
hay A=1 + 4 + 9 + 16 + ... + N2
Viết công thức tổng quát vd: n*n+1. (không dùng sigma)
Cho dãy số
a
n
xác định bởi
a
1
5
a
n
+
1
q
....
Đọc tiếp
Cho dãy số a n xác định bởi a 1 = 5 a n + 1 = q . a n + 3 với mọi n ≥ 1 trong đó q là hằng số, a ≠ 0 , q ≠ 1 . Biết công thức số hạng tổng quát của dãy số viết được dưới dạng a n = α . q n − 1 + β 1 − q n − 1 1 − q . Tính α + 2 β
A. 13
B. 9
C. 11
D. 16
Cho một cấp số cộng
u
n
có
u
1
5
và tổng 50 số hạng đầu bằng 5150. Tìm công thức của số hạng tổng quát
u
n
Đọc tiếp
Cho một cấp số cộng u n có u 1 = 5 và tổng 50 số hạng đầu bằng 5150. Tìm công thức của số hạng tổng quát u n
Thể tích của khối chóp có diện tích mặt đáy bằng B, chiều cao bằng h được tính bởi công thức: A.
V
1
3
B
.
h
B. VB.h C.
V
1
2
B
.
h
D. V3B.h
Đọc tiếp
Thể tích của khối chóp có diện tích mặt đáy bằng B, chiều cao bằng h được tính bởi công thức:
A. V = 1 3 B . h
B. V=B.h
C. V = 1 2 B . h
D. V=3B.h
Cho khối lăng trụ có thể tích V và chiều cao h. Khi đó diện tích S của đáy được tính theo công thức
Đọc tiếp
Cho khối lăng trụ có thể tích V và chiều cao h. Khi đó diện tích S của đáy được tính theo công thức
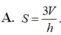
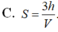
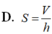
Một kim tự tháp Ai Cập được xây dựng khoảng 2500 năm trước công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao 150m, cạnh đáy dài 220m. Hỏi diện tích xung quanh của kim tự tháp đó bằng bao nhiêu? ( Diện tích xung quanh của hình chóp là tổng diện tích của các mặt bên).
Đọc tiếp
Một kim tự tháp Ai Cập được xây dựng khoảng 2500 năm trước công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao 150m, cạnh đáy dài 220m. Hỏi diện tích xung quanh của kim tự tháp đó bằng bao nhiêu? ( Diện tích xung quanh của hình chóp là tổng diện tích của các mặt bên).
Công thức tính diện tích xung quanh
S
x
q
của hình nón có đường sinh l, bán kính đáy r là
Đọc tiếp
Công thức tính diện tích xung quanh S x q của hình nón có đường sinh l, bán kính đáy r là
