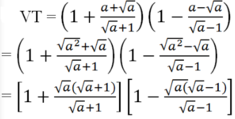
= (1 + √a)(1 - √a)
= 1 - (√a)2 = 1 - a = VP (đpcm)
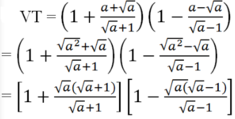
= (1 + √a)(1 - √a)
= 1 - (√a)2 = 1 - a = VP (đpcm)
Chứng minh các đẳng thức sau: 1 - a a 1 - a + a 1 - a 1 - a 2 = 1 v ớ i ≥ 0 v à a ≠ 1
Chứng minh các đẳng thức sau:
a ) 1 − a a 1 − a + a 1 − a 1 − a 2 = 1 v ớ i a ≥ 0 v à a ≠ 1 b ) a + b b 2 a 2 b 4 a 2 + 2 a b + b 2 = | a | v ó i a + b > 0 v à b ≠ 0
Chứng minh các đẳng thức sau:
a ) 2 3 − 6 8 − 2 − 216 3 ⋅ 1 6 = − 1 , 5 b ) 14 − 7 1 − 2 + 15 − 5 1 − 3 : 1 7 − 5 = − 2 c ) a b + b a a b : 1 a − b = a − b v ó i a , b d ư ơ n g v à a ≠ b . d ) 1 + a + a a + 1 ⋅ 1 − a − a a − 1 = 1 − a v ó i a ≥ 0 v à a ≠ 1
Chứng minh đẳng thức sau:
\(\left(\dfrac{1}{a-\sqrt{a}}+\dfrac{1}{\sqrt{a}-1}\right):\left(\dfrac{\sqrt{a}+1}{a-2\sqrt{a}+1}\right)=\dfrac{\sqrt{a}-1}{\sqrt{a}}\) với a>0 và a khác 1
chứng minh bất đẳng thức sau ;
\(\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right)\ge8\) với \(\left(\forall a,b,c>0\right)\)
các bạn giải chi tiết ra giùm mình nhé! cảm ơn nhiều à nhen !
CHỨNG MINH CÁC BẤT ĐẲNG THỨC SAU
a)Cho a>0 chứng minh \(a+\frac{1}{a}>=2\)
Chứng minh đẳng thức
1 a - a + 1 a - 1 : a + 1 a - 2 a + 1 = a - 1 a với a > 0, a ≠ 1
Cho 0 <x< 90 0 . Chứng minh các đẳng thức sau:
a, sin 4 x + cos 4 x = 1 - 2 sin 2 x cos 2 x
b, sin 6 x + cos 6 x = 1 - 3 sin 2 x cos 2 x
1. chứng minh rằng các hằng đẳng thức sau với điều kiện các biểu thức tồn tại:
a) \(\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\dfrac{1}{\sqrt{a}-\sqrt{b}}=a-b\)
b)\(\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)=1-a\)