sao cậu ko lấy sách ra mà chép
chứng minh ra chứ trong sách có 1 cái thôi còn 2 cái nữa mà
mn ơi giúp tớ với ạ :<
2 bài này con em tớ nó cứ hỏi mà tớ k biết lm ;-;
bài 1: tìm x:
x phần 20= 5 phần x
bài 2:
cho tam giác ABC có AB=AC; D là điểm bất kì trên cạnh AB. Tia p/giác của góc A cắt cạnh DC ở M, cắt cạnh BC ở I.
a) Chứng minh CM=BM.
b) Chứng minh AI là đường trung trực của đoạn thẳng BC.
c) từ D kẻ DH vuông góc với BC( H thuộc BC). Chứng minh góc BAC=2 BDH.
Ai làm nhanh nhất ib mình có quà ạ.
Cho tam giác ABC vuông tại A, có AB = AC. Gọi K là trung điểm của BC. a) Chứng minh tam giác AKB = tam giác AKC và AK vuông góc BC. b) Từ C kẻ đường vuông góc với BC, nó cắt AB tại E. Chứng minh EC // AK. c) Chứng Minh CE = CB
mn giúp tớ vs tớ đg cần gấp lm đây là bài tớ phải nộp cho thầy r!! GIÚP TỚ NHÉ!!!THANK YOU VERY MUCH!!! <3 <3 <3
Cho tam giác ABC, Am là tia phân giác của góc ngoài tại đỉnh A
a) biết AB = AC. Chứng minh Am // BC
b) biết Am // BC. Chứng minh AB = AC
Giúp mình với! mai nộp bài này rồi
giúp mình giải bài toán này vs. Mình thank nhoa!!!!
Cho tam giác ABC có AB=AC. Gọi E là trung điểm của BC.
a) Chứng minh tam giác AEB= tam giác AEC
b) Đường thẳng đi qua B vuông góc với BC cắt đường thẳng AC tại M. Chứng minh: BM//AE
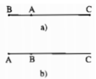
Một cách chứng minh khác của bất đẳng thức tam giác:
Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. Kẻ đường vuông góc AH đến đường thẳng BC (H thuộc BC).
Dùng nhận xét về cạnh lớn nhất trong tam giác vuông ở Bài 1 để chứng minh AB + AC > BC.
Chứng minh “Bất đẳng thức tam giác mở rộng ”: Với ba điểm A, B, C bất kỳ, ta có AB + AC ≥ BC
Bài 1: Cho tam giác ABC có AB= AC. Tia phân giác của góc A cắt BC tại M
a)Chứng minh: tam giác AMB = tam giác AMC
b)Chứng minh: M là trung điểm của BC
c) K là 1 điểm bất kì trên đoạn thẳng AM, đường thẳng CK cắt cạnh AB tại I. Vẽ IH vuông góc với BC tại H. Chứng minh góc BAC = góc 2BIH
Giúp mk nha mai mk phải nộp bÌ rồi
Cho tam giác ABC. Chứng minh bất đẳng thức sau:
a) AB + BC > AC.
b) AC + BC > AB.
Chứng minh bất đẳng thức của tam giác
AB+BC>AC
AC+BC >AB
