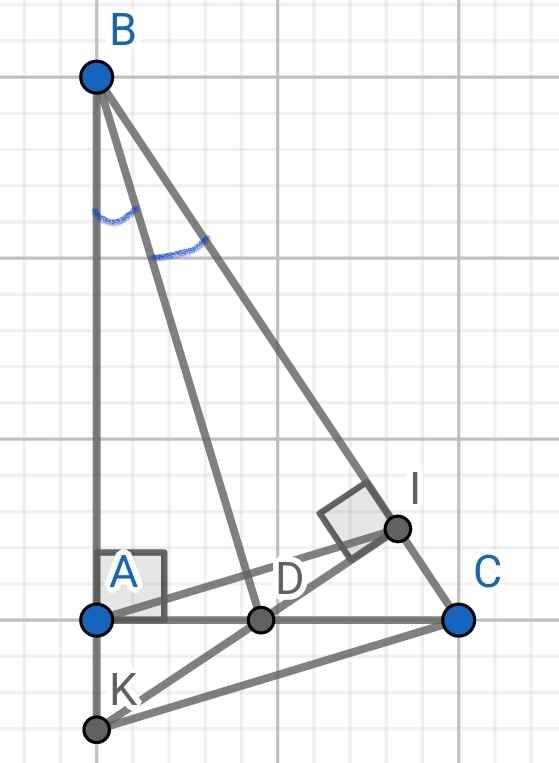
a) Xét hai tam giác vuông: ∆ABD và ∆IBD có:
BD chung
∠ABD = ∠IBD (gt)
⇒ ∆ABD = ∆IBD (cạnh huyền - góc nhọn)
b) Do ∆ABD = ∆IBD (cmt)
⇒ AD = ID (hai cạnh tương ứng)
∆DIC vuông tại I
⇒ DC là cạnh huyền
⇒ ID < DC
Mà AD = ID (cmt)
⇒ AD < DC
c) Xét hai tam giác vuông: ∆DAK và ∆DIC có:
AD = ID (cmt)
∠ADK = ∠IDC (đối đỉnh)
⇒ ∆DAK = ∆DIC (cạnh góc vuông - góc nhọn kề)
⇒ DK = DC (hai cạnh tương ứng)
d) Do ∆DAK = ∆DIC (cmt)
⇒ AK = IC (hai cạnh tương ứng)
Do ∆ABD = ∆IBD (cmt)
⇒ AB = IB (hai cạnh tương ứng)
∆ABI cân tại B
⇒ ∠BAI = ∠BIA = (180⁰ - ∠ABC)/2 (1)
Do AB = IB (cmt)
AK = IC (cmt)
⇒ BK = BC
⇒ ∆BCK cân tại B
⇒ ∠BKC = ∠BCK = (180⁰ - ∠ABC)/2 (2)
Từ (1) và (2) ⇒ ∠BAI = ∠BKC
Mà ∠BAI và ∠BKC là hai góc đồng vị
⇒ AI // KC












