Các câu hỏi tương tự
Cho x, y là các số thực dương thỏa mãn 9ln2 x + 4ln2 y = 12ln x.ln y. Đẳng thức nào sau đây là đúng?
A. x2 = y3
B. 3x = 2y
C. x3 = y2
D. x = y
Cho hàm số
y
ln
2
x
-
a
-
2
m
ln
2
x
-
a
+
2
(m là tham số thực), trong đó x,...
Đọc tiếp
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 x 2 + a 2 - 2 n - 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 , e 2 y = 1 . Số phần tử của S là:
A. 0
B. 1
C. 2
D. Vô số
Cho các số thực dương x; y thỏa mãn x2 + y2 14. Khẳng định nào sau đây là đúng ? A.
log
2
x
+
y
14
log
2
x+
log
2
y B.
log
2
x
+
y...
Đọc tiếp
Cho các số thực dương x; y thỏa mãn x2 + y2 = 14. Khẳng định nào sau đây là đúng ?
A. log 2 x + y 14 = log 2 x+ log 2 y
B. log 2 x + y 16 =x+ log 2 y
C. log 2 ( x + y ) = log 2 x + log 2 y 2
D. log 2 x + y = 2 + log 2 x y 2
Cho hàm số
y
ln
(
2
x
-
a
)
-
2
m
ln
(
2
x
-
a
)
+...
Đọc tiếp
Cho hàm số y = ln ( 2 x - a ) - 2 m ln ( 2 x - a ) + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + . . . + log . . . 2 ( x 2 + a 2 ) - ( 2 n + 1 - 1 ) ( log 2 x a + 1 ) = 0
(với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thoả mãn m a x [ 1 ; e 2 ] y = 1 . Số phần tử của S là
A. 0
B. 1
C. 2
D. Vô số
Cho các số thực dương x; y 0 thỏa mãn x2 + y2 8xy. Khẳng định nào sau đây là đúng ? A.
log
(
x
+
y
)
1
+
log
x
+
log
y
2
B. log( x + y) logx + log y + 1 C. log(x + y) logx + logy - 1 D. log(x + y) 10( logx + logy)
Đọc tiếp
Cho các số thực dương x; y > 0 thỏa mãn x2 + y2 = 8xy. Khẳng định nào sau đây là đúng ?
A. log ( x + y ) = 1 + log x + log y 2
B. log( x + y) = logx + log y + 1
C. log(x + y) = logx + logy - 1
D. log(x + y) = 10( logx + logy)
Trong mặt phẳng tọa độ Oxyz, gọi
(
H
1
)
là hình phẳng giới hạn bởi các đường
y
x
2
4
;
y
-
x
2
4
; x4; x -4 và
(
H
2
)...
Đọc tiếp
Trong mặt phẳng tọa độ Oxyz, gọi ( H 1 ) là hình phẳng giới hạn bởi các đường y = x 2 4 ; y = - x 2 4 ; x=4; x = -4
và ( H 2 ) là hình gồm tất cả các điểm (x;y) thỏa mãn x 2 + y 2 ≤ 16 ; x 2 + ( y - 2 ) 2 ≥ 4 ; x 2 + ( y + 2 ) 2 ≥ 4
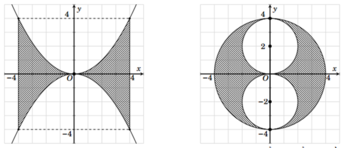
Cho H 1 và H 2 quay quanh trục Oy ta được các vật thể có thể tích lần lượt là V 1 , V 2 . Đẳng thức nào sau đây đúng?
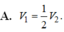
![]()
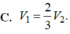
![]()
Cho các số thực x y z thỏa mãn.Có bao nhiêu giá trị nguyên của z để có đúng 2 cặp (x;y) thỏa mãn đẳng thức trên:A.2B.211C.99D.4
Đọc tiếp
Cho các số thực x y z thỏa mãn.Có bao nhiêu giá trị nguyên của z để có đúng 2 cặp (x;y) thỏa mãn đẳng thức trên:
A.2
B.211
C.99
D.4
Cho x, y là các số thực dương thỏa mãn
ln
x
+
ln
y
≥
ln
(
x
2
+
y
)
là các số thực dương thỏa mãn
P
x
+
y
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn ln x + ln y ≥ ln ( x 2 + y ) là các số thực dương thỏa mãn P = x + y
![]()
![]()
![]()
![]()
Cho x, y là các số thực dương thỏa mãn điều kiện
5
x
+
2
y
+
3
3
x
y
+
x
+
1
5
x
y
5
+...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn điều kiện 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 - x - 2 y + y ( x - 2 ) .Tính giá trị nhỏ nhất của biểu thức T = x + y
![]()
![]()
![]()
![]()





