Các câu hỏi tương tự
cho a,b,c là độ dài 3 cạnh của 1 tam giác và x,y,z là độ dài 3 đường phân giác của tam giác đó. CMR \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}>\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)
Cho a,b,c là độ dài các cạnh của một tam giác, ma, mb, mc là độ dài các đường trung tuyến của tam giác đó. Chứng minh rằng
\(\dfrac{a}{m_a}+\dfrac{b}{m_b}+\dfrac{c}{m_c}\ge\dfrac{\sqrt{3}}{2}\)
Tam giác ABC có các cạnh a = 8cm, b = 10cm và c = 13cm.
a) Tam giác đó có góc tù không?
b) Tính độ dài trung tuyến MA của tam giác ABC đó.
Trong mặt phẳng tọa độ Oxy cho tam giác ABC có trực tâm H, trọng tâm G(-1;3). Gọi K, M, N lần lượt là trung điểm của AH, AB, AC. Tìm phương trình đường tròn ngoại tiếp tam giác ABC biết rằng đường tròn ngoại tiếp tam giác KMN là (C): x2+y2+4x-4y-17=0.
Cho tam giác ABC có \(\frac{\sin B+2018\sin C}{2018\cos B+\cos C}=\sin A\)và độ dài các cạnh là các số tự nhiên. Gọi M là trung điểm của cạnh BC và G là trọng tâm tam giác ABC. Chứng minh rằng tam giác MBG có diện tích là một số tự nhiên
LÀM HỘ MK NHA!!!
THANKS!!!
Cho tam giác ABC có a,b,c,ma,mb,mc,R lần lượt là độ dài các cạnh BC,CA,AB, độ dài các đường trung tuyến kẻ từ A,B,C và bán kính đường tròn ngoại tiếp tam giác. Biết rằng: \(\frac{a^2+b^2}{mc}+\frac{b^2+c^2}{ma}+\frac{c^2+a^2}{mb}=12R\). Chứng minh rằng tam giác ABC đều
Câu 6: Cho tàm giác ABC có A(1; - 1) ;B(2; 0) ;C(3; 5) a) Tìm tọa độ các vecto AB ,AC ,BC b) Tính độ dài các cạnh của tam giác ABC. Từ đó tính chu vi tam giác. c) Tìm tọa độ trung điểm các cạnh và tìm tọa độ trọng tâm của tam giác ABC. d) Tìm tọa độ điểm D để tứ giác ABCD là hnh bình hành e) Tọa độ chân đường cao xuất phát từ A của tam giác. Đ) Tính góc A?
Cho a,b,c là độ dài 3 cạnh của tam giác có chu vi bằng 3. Chứng minh rằng:
\(\frac{a}{1+b^2}+\frac{b}{1+c^2}+\frac{c}{1+a^2}\ge\frac{3}{2}\)
Trong mặt phẳng với hệ tọa độ Oxy, cho elíp :
E
:
x
2
4
+
y
2
1
và điểm C( 2;0) .Tìm tọa độ các điểm A; B trên (E), biết rằng hai điểm đối xứng nhau qua trục hoành và tam giác ABC là tam giác đều và điểm A có tung độ dương .
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho elíp : E : x 2 4 + y 2 = 1 và điểm C( 2;0) .Tìm tọa độ các điểm A; B trên (E), biết rằng hai điểm đối xứng nhau qua trục hoành và tam giác ABC là tam giác đều và điểm A có tung độ dương .
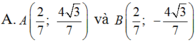
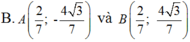
![]()