Chọn C.
Ta có: logxyz( y3z2) = 3logxyzy + 2logxyzz
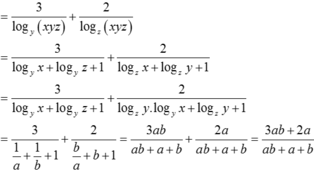
Chọn C.
Ta có: logxyz( y3z2) = 3logxyzy + 2logxyzz
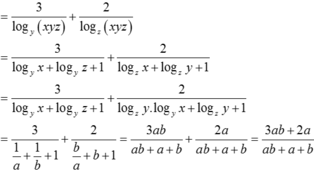
Giả sử a, b là các số thực sao cho x3 + y3 = a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) = z và log(x2 + y2) = z + 1. Giá trị của a+b bằng:
A. - 31 2
B. - 25 2
C. 31 2
D. 29 2
Cho các số thực x, y, z thỏa mãn y = 10 1 1 - log x , z = 10 1 1 - log y . Mệnh đề nào sau đây đúng?
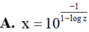
![]()
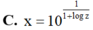
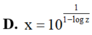
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn ( x + 3 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 2 và a+b+c=1. Giá trị nhỏ nhất của biểu thức P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 là
A. 3 - 2
B. 3 + 2
C. 5 - 2 6
D. 5 + 2 6
Cho a , b , c , x , y , z là các số thực thay đổi thỏa mãn ( x + 1 ) 2 + ( y + 1 ) 2 + ( z - 2 ) 2 = 4 và a + b + c = 6 . Tính giá trị nhỏ nhất của P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 . .
![]()
![]()
![]()
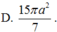
Với các số thực dương x,y tùy ý , đặt log 3 x = a , log 3 y = b . Mệnh đề nào dưới đây là đúng ?
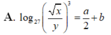
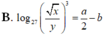
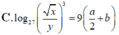
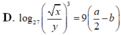
P557(Mức A)Cho a,b,c là các số thực dương tuỳ ý,và cho x,y,z là các số thực dương có tổng bằng 1.Đặt:M=max{a,b,c}và m=min{x,y,z}.chứng minh rằng:\(M-\left(xa+yb+zc\right)\ge\frac{m}{2}\left(\left(\sqrt{a}-\sqrt{b}\right)^2+\left(\sqrt{b}-\sqrt{c}\right)^2+\left(\sqrt{c}-\sqrt{a}\right)^2\right).\)
Cho a là số thực tùy ý và b, c là các số thực dương khác 1.
Hình vẽ bên là đồ thị của ba hàm số y = x a , y = log b x , y = log c x , x > 0 .
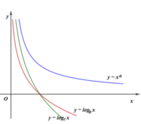
Khẳng định nào sau đây đúng?
A. a < c < b
B. a > c > b
C. a > b > c
D. a < b < c
Cho số phức z = a + bi (với a,b là các số thực). Xét các phát biểu sau:
1:\(z^2-\overline{z}^2\) là số thực
2:\(z^2+\overline{z^2}\) là số ảo
3:\(z.\overline{z}\) là số thực
4:\(\left|z\right|-z\) bằng 0
Có bao nhiêu mệnh đề đúng?
A:0
B:1
C:2
D:3
Với a, b là các số thực dương tùy ý và a khác 1, đặt P = log a b 3 + log a 2 b 6 Mệnh đề nào dưới đây đúng ?
A. P = 9 log a b
B. P = 27 log a b 15
C. P = 15 log a b
D. P = 6 log a b