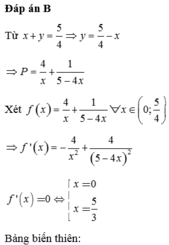Các câu hỏi tương tự
cho hàm số y=X4-2mx2+m(C) với m là tham số thực.Gọi A là điểm thuộc đồ thị (C) có hoành độ bằng 1.tìm tham số m để tiếp tuyến đenta với đồ thị (C) tại A cắt đường tròn (T): x2+(y-1)2=4 tạo thành dây cung có độ dài nhỏ nhất
A.m=16/13
B.-13/16
C.13/16
D.-16/13
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn
(
x
+
3
)
2
+
(
y
-
2
)
2
+
(
z
+
1
)...
Đọc tiếp
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn ( x + 3 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 2 và a+b+c=1. Giá trị nhỏ nhất của biểu thức P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 là
A. 3 - 2
B. 3 + 2
C. 5 - 2 6
D. 5 + 2 6
Cho (P):
y
x
2
+
2
x
-
3
và d: y m(x - 4) - 2. Tìm m để d cắt (P) tại hai điểm
A
x
1
;
y
1
;
B
x
2
;
y
2...
Đọc tiếp
Cho (P): y = x 2 + 2 x - 3 và d: y = m(x - 4) - 2. Tìm m để d cắt (P) tại hai điểm A x 1 ; y 1 ; B x 2 ; y 2 sao cho biểu thức P = 2 x 1 2 + x 2 2 + 9 x 1 x 2 + 2014 đạt giá trị nhỏ nhất
![]()
![]()
![]()
![]()
Cho hai số thực
x
,
y
thỏa mãn
0
≤
x
≤
1
2
,
0
y
≤
1
và
log
(
11
-
2
x
-
y
)
2
x
+
4
y
-
1
...
Đọc tiếp
Cho hai số thực x , y thỏa mãn 0 ≤ x ≤ 1 2 , 0 < y ≤ 1 và log ( 11 - 2 x - y ) = 2 x + 4 y - 1 Xét biểu thức P = 16 x 2 y - 2 x ( 3 y + 2 ) - y + 5 . Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của biểu thức T = 4 m + M bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
Cho a , b , c , x , y , z là các số thực thay đổi thỏa mãn
(
x
+
1
)
2
+
(
y
+
1
)
2
+...
Đọc tiếp
Cho a , b , c , x , y , z là các số thực thay đổi thỏa mãn ( x + 1 ) 2 + ( y + 1 ) 2 + ( z - 2 ) 2 = 4 và a + b + c = 6 . Tính giá trị nhỏ nhất của P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 . .
![]()
![]()
![]()
Trong không gian Oxyz cho mặt cầu
(
S
)
:
(
x
-
2
)
2
+
(
y
-
1
)
2
+
(
z
-
1
)
2...
Đọc tiếp
Trong không gian Oxyz cho mặt cầu ( S ) : ( x - 2 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 9 và điểm M ( a ; b ; c ) ∈ ( S ) sao cho biểu thức P=2a+2b+2c đạt giá trị nhỏ nhất. Tính T=a+b+c.
A. 2
B. 1
C. -2
D. -1
Trong không gian với hệ trục tọa độ Oxyz cho 3 điểm A (1; 1; 1), B (0; 1; 2), C (-2; 1; 4) và mặt phẳng (P): x - y + z + 2 0. Tìm điểm N ∈ (P) sao cho S NA2 + NB2 + NC2 đạt giá trị nhỏ nhất.
A
.
N
-
4
3
;
2
;
4...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho 3 điểm A (1; 1; 1), B (0; 1; 2), C (-2; 1; 4) và mặt phẳng (P): x - y + z + 2 = 0. Tìm điểm N ∈ (P) sao cho S= NA2 + NB2 + NC2 đạt giá trị nhỏ nhất.
A . N - 4 3 ; 2 ; 4 3
B. N (-2; 0; 1)
C . N - 1 2 ; 5 4 ; 3 4
D. N (-1; 2; 1)
Cho x, y 0 thỏa mãn
x
+
y
3
2
và biểu thức
P
4
x
+
1
4
y
đạt giá trị nhỏ nhất. Tính
x
2
+
y
2
A.
25
16...
Đọc tiếp
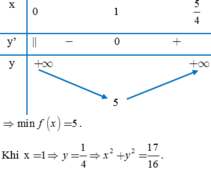
Cho x, y > 0 thỏa mãn x + y = 3 2 và biểu thức P = 4 x + 1 4 y đạt giá trị nhỏ nhất. Tính x 2 + y 2
A. 25 16
B. 5 4
C. 2313 1156
D. 153 100
Cho hai số thực x,y thỏa mãn điều kiện:`x^4+y^4+6x^2y^2+2=2x^2+3y^2`
Tính giá trị lớn nhất và nhỏ nhất của `P=(-6x^2-5y^2-4x^2y^2-7)/(x^2+y^2+1)`
Thầy Lâm cứu em :<<