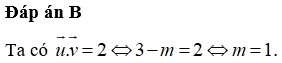Các câu hỏi tương tự
Trong không gian với hệ trục tọa độ Oxyz, cho ba vectơ
u
→
1
;
1
;
2
,
a
→
3
;
-
1
;
-
2
và
v
→...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho ba vectơ u → = 1 ; 1 ; 2 , a → = 3 ; - 1 ; - 2 và v → = - 1 ; m ; m - 2 . Để vectơ u → , v → vuông góc với a → thì giá trị m bằng bao nhiêu?
A. m = 2
B. m = -2
C. m = 1
D. m = -1
Trong không gian với hệ tọa độ
O
,
i
→
,
j
→
,
k
→
cho 2 điểm A,B thỏa mãn
O
A
→
2
i
→
-
j...
Đọc tiếp
Trong không gian với hệ tọa độ O , i → , j → , k → cho 2 điểm A,B thỏa mãn O A → = 2 i → - j → + k → và O B → = i → + j → - 3 k → . Tìm tọa độ trung điểm M của đoạn thẳng AB
A. M 1 2 ; 0 ; - 1
B. M 3 2 ; 0 ; - 1
C. M(3;4;-2)
D. M 1 2 ; - 1 ; 2
Cho các vecto
i
→
,
j
→
,
k
→
không đồng phẳng. Xét các vecto
u
→
2
i
→
-
j
→
+
k
→
,
v
→
i
→
-...
Đọc tiếp
Cho các vecto i → , j → , k → không đồng phẳng. Xét các vecto u → = 2 i → - j → + k → , v → = i → - 2 j → - k → , w → = x i → + 3 j → + 2 k → x ∈ R . Tìm x sao cho ba vecto u → , v → , w → đồng phẳng
A. x = -1
B. x = 1
C. x = -2
D. x = 2
1. Cho hàm số y2x-1/x-1 . Lấy M thuộc C với XMm . tiếp tuyến của C tại M cắt 2 đường tiệm cận tại A,B . Gọi I là giao của 2 đường tiệm cận . CMR : M là trung điểm của AB và tam giác IAB có diện tích không phụ thuộc vào M 2.cho yx+2/x-3 tìm M thuộc C sao cho khoảng cách từ M đến 2 đường tiệm cận C bằng nhau 3. cho y x+2/x-2 tìm M thuộc C sao cho M cách đều hai trục tọa độ . viết pttt của C biết tiếp tuyến đó đi qua A(-6;5) 4 . cho y x+1/x-1 . CMR (d) : 2x-y+m0 luôn cắt C tại A,B trên 2 nhánh củ...
Đọc tiếp
1. Cho hàm số y=2x-1/x-1 . Lấy M thuộc C với XM=m . tiếp tuyến của C tại M cắt 2 đường tiệm cận tại A,B . Gọi I là giao của 2 đường tiệm cận . CMR : M là trung điểm của AB và tam giác IAB có diện tích không phụ thuộc vào M
2.cho y=x+2/x-3 tìm M thuộc C sao cho khoảng cách từ M đến 2 đường tiệm cận C bằng nhau
3. cho y = x+2/x-2 tìm M thuộc C sao cho M cách đều hai trục tọa độ . viết pttt của C biết tiếp tuyến đó đi qua A(-6;5)
4 . cho y = x+1/x-1 . CMR (d) : 2x-y+m=0 luôn cắt C tại A,B trên 2 nhánh của (C) . tìm m để AB ngắn nhất
1, Cho tg ABC có A90 . Gọi I là TĐ của cạnh AC . Trên tia đối của tia IB lấy điểm D/ IBID. Nối C với D a, CMR tg AIB tg CID b, Gọi M là Tđ Của BC, N là TĐ của AD CMR I là TĐ cuar MN c, Cmr góc AIBBIC Tìm đk tg ABC để AC vuông CD2, Cho tam giác ABC gọi M là TĐ của cạnh BC . Trên tia đối của MA lấy điểm E sao cho MEMA CMR: a,ACBE và AD // BE b, Gọi I là 1 điểm của bk AC, Gọi K là 1 điểm trên BE / AIEK. CMR 3 điểm I,M,K thẳng hàng c, Từ EH vg BC tại H biết HBE50 MEB25 Tính HEM và BME
Đọc tiếp
1, Cho tg ABC có A<90 . Gọi I là TĐ của cạnh AC . Trên tia đối của tia IB lấy điểm D/ IB=ID. Nối C với D a, CMR tg AIB= tg CID b, Gọi M là Tđ Của BC, N là TĐ của AD CMR I là TĐ cuar MN c, Cmr góc AIB<BIC Tìm đk tg ABC để AC vuông CD
2, Cho tam giác ABC gọi M là TĐ của cạnh BC . Trên tia đối của MA lấy điểm E sao cho ME=MA CMR: a,AC=BE và AD // BE b, Gọi I là 1 điểm của bk AC, Gọi K là 1 điểm trên BE / AI=EK. CMR 3 điểm I,M,K thẳng hàng c, Từ EH vg BC tại H biết HBE=50 MEB=25 Tính HEM và BME
đường kính và bán kính của mặt trời
Sao diêm vương và Nga nơi nào có diện tích rộng hơn
Trái đất quay được bao nhiêu vòng quanh mặt trời
1 mi crô mét = ? Km
Cho hàm số
y
2
x
-
3
x
-
3
(C). Gọi I là giao điểm của hai tiệm cận. Tìm điểm M thuộc (C). Biết tiếp tuyến của (C) tại M cắt các đường tiệm cận tại J và K sao cho đường tròn ngoại tiếp tam giác IJK có diện tích lớn nhất. A. M ( 1;1 ); M ( 3;3 ) B.
M
0
;...
Đọc tiếp
Cho hàm số y = 2 x - 3 x - 3 (C). Gọi I là giao điểm của hai tiệm cận. Tìm điểm M thuộc (C). Biết tiếp tuyến của (C) tại M cắt các đường tiệm cận tại J và K sao cho đường tròn ngoại tiếp tam giác IJK có diện tích lớn nhất.
A. M ( 1;1 ); M ( 3;3 )
B. M 0 ; 3 2 , M 4 ; 5 2
C. M 1 ; 1 , M 0 ; 3 2
D. M 3 ; 3 , M 4 ; 5 2
Một học sinh giải bài toán “Tìm tất cả các giá trị thực của tham số m sao cho hàm số
y
m
x
3
+
m
x
2
+
m
−
2
x
+
10
đồng biến trên i” theo các bước như sau:Bước 1: Hàm số xác định trên i, và
y
3
m
x...
Đọc tiếp
Một học sinh giải bài toán “Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m x 3 + m x 2 + m − 2 x + 10 đồng biến trên i” theo các bước như sau:
Bước 1: Hàm số xác định trên i, và y ' = 3 m x 2 + 2 m x + m − 2
Bước 2: Yêu cầu bài toán tương đương với y ' > 0, ∀ x ∈ ℝ ⇔ 3 m x 2 + 2 m x + m − 2 > 0, ∀ x ∈ ℝ
Bước 3: ⇔ a = 3 m > 0 Δ ' = 6 m − 2 m 2 < 0 ⇔ m < 0 m > 3 m > 0
Bước 4: ⇔ m > 3. Vậy m>3
Hỏi học sinh này đã bắt đầu sai ở bước nào?
A. Bước 2
B. Bước 3
C. Bước 1
D. Bước 4
Trong không gian với hệ tọa độ Oxyz, cho 3 vectơ
a
→
1
;
m
;
2
,
b
→
m
+
1
;
2
;
1
,
c
→...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho 3 vectơ a → = 1 ; m ; 2 , b → = m + 1 ; 2 ; 1 , c → = 0 ; m − 2 ; 2 . Điều kiện của m để 3 vectơ đã cho đồng phẳng là
A. m = 0
B. m = 2 5 m = 1
C. m = 1
D. m = 2 5