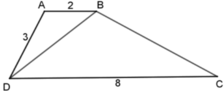
Vì ΔABD ⁓ ΔBDC nên A B B D = B D D C = A D B C , tức là 2 B D = B D 8 = 3 B C
Ta có B D 2 = 2.8 = 16 nên BD = 4 cm
Suy ra BC = 8.3 4 = 6 cm
Vậy BD = 4cm, BC = 6cm
Đáp án: D
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Tứ giác ABCD có
A
B
3
c
m
,
B
C
10
c
m
,
C
D
12
c
m
,
A
D
5
c
m
v
à
B
D
6
c
m
Chứng minh:a)
Δ
A
B
D
∽
Δ...
Đọc tiếp
Tứ giác ABCD có A B = 3 c m , B C = 10 c m , C D = 12 c m , A D = 5 c m v à B D = 6 c m Chứng minh:
a) Δ A B D ∽ Δ B D C ; b) ABCD là hình thang
Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng ΔABD ⁓ ΔBDC. Cho AB = 2cm, AD = 3cm, CD = 8cm. Tính đọ dài cạnh còn lại của tứ giác ABCD.
A. BC = 6cm
B. BC = 4cm
C. BC = 5cm
D. BC = 3cm
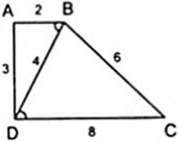
Tứ giác ABCD có AB = 2cm; BC = 6cm; CD = 8cm; DA = 3cm và BD = 4cm. Chứng minh rằng: ABCD là hình thang
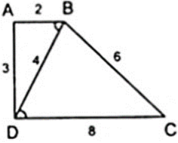
Tứ giác ABCD có AB = 2cm; BC = 6cm; CD = 8cm; DA = 3cm và BD = 4cm. Chứng minh rằng: ABCD là hình thang
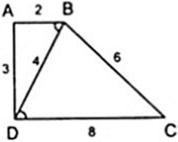
Cho tứ giác ABCD có AB = 3cm ; BC = 10cm ; CD = 12cm ; AD = 5cm, đường chéo BD = 6cm. Chứng minh rằng
a) Tam giác ABD đồng dạng với tam giác BCD
b) ABCD là hình thang
Tứ giác ABCD có AB = 2cm; BC = 6cm; CD = 8cm; DA = 3cm và BD = 4cm. Chứng minh rằng: Δ BAD ∼ Δ DBC
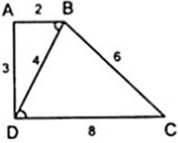
Tứ giác ABCD có AB = 2cm; BC = 6cm; CD = 8cm; DA = 3cm và BD = 4cm. Chứng minh rằng: Δ BAD ∼ Δ DBC
Tứ giác ABCD có AB = 3cm, BC = 10cm, CD = 12cm, AD = 5cm,
đường chéo BD = 6cm.
Chứng minh rằng :
a) Tam giác ABD đồng dạng tam giác BDC rồi suy ra BD2=AB.CD
b) Tứ giác ABCD là hình thang.
Cho tứ giác ABCD có AB=3cm. BC=10cm, CD=12cm. AD = 5cm và BD=6cm. Chứng minh:
a) Tam giác ABD đồng dạng với tam giác BDC.
b) ABCD là hình thang.