Đáp án C
Cách 1.
Gọi N là trung điểm của AC ⇒ M N / / A B
![]()
Cho OA =OB =OC =1. Ta có.

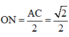
Vậy ∆ O M N là tam giác đều và O M N = 60 o
Cách 2. Dùng pp tọa độ hóa và công thức

Đáp án C
Cách 1.
Gọi N là trung điểm của AC ⇒ M N / / A B
![]()
Cho OA =OB =OC =1. Ta có.

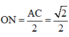
Vậy ∆ O M N là tam giác đều và O M N = 60 o
Cách 2. Dùng pp tọa độ hóa và công thức

Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc với nhau và Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng
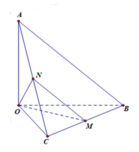
A. 90 0
B. 30 0
C. 60 0
D. 45 0
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA=OB=OC=a. Khoảng cách giữa hai đường thẳng OA và BC bằng
A. a
B. a 2
C. a 2 2
D. a 3 2
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau, OA = a 2 2 , OB=OC=a. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC). Tính thể tích khối tứ diện OABH.
A. a 3 2 6
B. a 3 2 12
C. a 3 2 24
D. a 3 2 48
Cho hình chóp S.ABC có ba cạnh OA, OB, OC đôi một vuông góc và OA = OB = OC = a. Gọi M là trung điểm cạnh AB . Góc hợp bởi hai véc tơ B C → và O M → bằng
A. 120 o
B. 150 o
C. 135 o
D. 60 o
Cho tứ diện ABCD có OA, OB, OC đôi một vuông góc với nhau và OA=OB=2OC. Gọi G là trọng tâm tam giác ABC. Góc giữa hai đường thẳng OG và AB bằng
A. 75°
B. 60°
C. 45°
D. 90°
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Biết OA=a, OB=2a và đường thẳng AC tạo với mặt phẳng (OBC) một góc 60 0 . Thể tích khối tứ diện OABC bằng
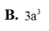
![]()
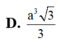
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với
nhau và OA = a, OB = 2a, OC = 3a. Thể tích của khối tứ
diện OABC bằng
A. V = 2 a 3 3
B. V = a 3 3
C. V = 2 a 3
D. V = a 3
Cho tứ diện OABC biết OA, OB, OC đôi một vuông góc với nhau, biết OA=3, OB=4 và thể tích khối tứ diện OABC bằng 6. Khi đó khoảng cách từ O đến mặt phẳng (ABC) bằng:
A. 3
B. 41 12
C. 144 41
D. 12 41
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA=a, OB=b, OC=c. Tính thể tích khối tứ diện OABC.
A. abc
B. abc/3
C. abc/2
D. abc/6