Chọn A

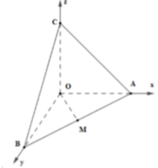
Gắn hệ trục tọa độ Oxyz như hình vẽ với
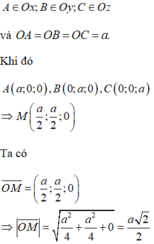
Và
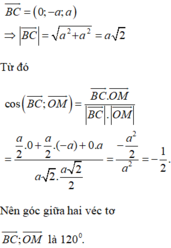
Chọn A


Gắn hệ trục tọa độ Oxyz như hình vẽ với
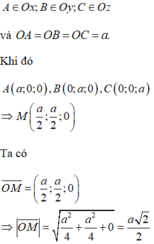
Và
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau, OA = a 2 2 , OB=OC=a. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC). Tính thể tích khối tứ diện OABH.
A. a 3 2 6
B. a 3 2 12
C. a 3 2 24
D. a 3 2 48
Cho hình chóp tam giác O.ABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = b, OC = c. Hãy tính đường cao OH của hình chóp.
Cho hình chóp O.ABC có OA, OB, OC đôi một vuông góc tại O và OA=2, OB=3, OC=6. Thể tích của khối chóp bằng:
A. 12
B. 6
C. 24
D. 36.
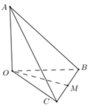
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA =OB= OC. Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng
A. 90 o
B. 30 o
C. 60 o
D. 45 o
Cho hình chóp O.ABC có OA=OB=OC=a, A O B ^ = 60 ° , B O C ^ = 90 ° , A O C ^ = 120 ° . Gọi S là trung điểm cạnh OB. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là
![]()
![]()
![]()
![]()
Cho khối chóp O.ABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Biết OA = 1, OB = 2 và thể tích khối chóp O.ABC bằng 3. Độ dài cạnh OC bằng:
A. 3 2
B. 9 2
C. 9
D. 3
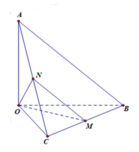
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc với nhau và Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng
A. 90 0
B. 30 0
C. 60 0
D. 45 0
Cho khối tứ diện OABC có OA, OB, OC đôi một vuông góc và OA=a, OB=b, OC=c. Thể tích V của khối tứ diện OABC được tính bởi công thức nào sau đây?
![]()
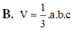
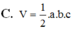
![]()
Cho tứ diện ABCD có OA, OB, OC đôi một vuông góc với nhau và OA=OB=2OC. Gọi G là trọng tâm tam giác ABC. Góc giữa hai đường thẳng OG và AB bằng
A. 75°
B. 60°
C. 45°
D. 90°