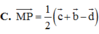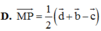Đáp án A
- Phương pháp: Sử dụng công thức 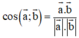
- Cách giải:
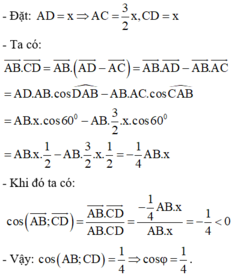
Đáp án A
- Phương pháp: Sử dụng công thức 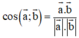
- Cách giải:
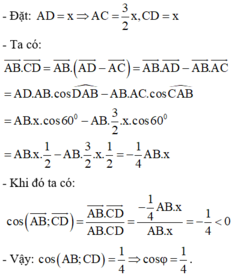
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a, gọi φ là góc giữa hai mặt phẳng (SAB) và (CSD) Tính cos φ
A. cos φ = 1 2
B. cos φ = 1 6
C. cos φ = 1 3
D. cos φ = 1 4
Cho tứ diện đều ABCD. Gọi φ là góc giữa hai mặt phẳng (BCD) và (ABC) Khẳng định nào sau đây là đúng?
![]()
![]()
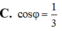
![]()
Cho tứ diện ABCD với A C = 2 3 A D , ∠ C A B = ∠ D A B = 60 ° , CD=AD .Gọi là góc giữa AB và CD. Chọn khẳng định đúng?
A. cos φ = 1 4
B. φ = 60 °
C. φ = 30 °
D. cos φ = 3 4
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AB = a, AC = a 3 Hình chiếu vuông góc của A' lên mặt phẳng (ABC) là trung điểm H của BC, HA' = a 5 Gọi φ là góc giữa hai đường thẳng A'B và B'C.
Tính cos φ
A.cos φ = 7 3 48
B. cos φ = 3 2
C. cos φ = 1 2
D. cos φ = 7 3 24
Hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D, có AB = 2a, AD = DC = a, có cạnh SA vuông góc với mặt phẳng (ABCD) và SA = a.
a) Chứng minh mặt phẳng (SAD) vuông góc với mặt phẳng (SDC), mặt phẳng (SAC) vuông góc với mặt phẳng (SCB).
b) Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABCD), tính tanφ.
c) Gọi (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC). Hãy xác định (α) và xác định thiết diện của hình chóp S.ABCD với (α)
Tứ diện ABCD có tam giác BCD đều cạnh a, AB vuông góc với mặt phẳng (BCD), AB = 2a. M là trung điểm của AD, gọi φ là góc giữa đường thẳng CM với mp(BCD), khi đó
A. tan φ = 3 2
B. tan φ = 2 3 3
C. tan φ = 3 2 2
D. tan φ = 6 3
Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a, có góc B A D ^ = 60 o và S A = S B = S D = a 3 2
a) Tính khoảng cách từ S đến mặt phẳng (ABCD) và độ dài cạnh SC.
b) Chứng minh mặt phẳng (SAC) vuông góc với mặt phẳng (ABCD).
c) Chứng minh SB vuông góc với BC.
d) Gọi φ là góc giữa hai mặt phẳng (SBD) và (ABCD). Tính tanφ.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a cạnh bên SA vuông góc mặt đáy và SA = a . Gọi φ là góc tạo bởi SB và mặt phẳng (ABCD). Xác định cot φ .
A. cot φ = 2
B. cot φ = 1 2
C. cot φ = 2 2
D. cot φ = 2 4
Cho tứ diện ABCD. Gọi M và P lần lượt là trung điểm của AB và CD. Đặt A B → = b → ; A C → = c → ; A D → = d . Khẳng định nào sau đây đúng?
![]()
![]()