Các câu hỏi tương tự
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng (AMN) luôn vuông góc với mặt phẳng (BCD). Gọi
V
1
;
V
2
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN. Tính
V
1
+
V
2
A.
17
2...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng (AMN) luôn vuông góc với mặt phẳng (BCD). Gọi V 1 ; V 2 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN. Tính V 1 + V 2
A. 17 2 216
B. 17 2 72
C. 17 2 144
D. 2 12
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng
A
M
N
luôn vuông góc với mặt phẳng
B
C
D
.
Gọi
V
1
;
V
2
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABM...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng A M N luôn vuông góc với mặt phẳng B C D . Gọi V 1 ; V 2 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN. Tính V 1 + V 2 ?
A. 17 2 216
B. 17 2 72
C. 17 2 144
D. 2 12
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V A.
11
2
a
3
216
B.
7...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V
A. 11 2 a 3 216
B. 7 2 a 3 216
C. 2 a 3 8
D. 13 2 a 3 216
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V. A.
11
2
a
3
216
B.
7
2...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V.
A. 11 2 a 3 216
B. 7 2 a 3 216
C. 2 a 3 18
D. 13 2 a 3 216
Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M, N lần lượt là trung điểm các cạnh AD, BD. Gọi P là điểm trên cạnh AB sao cho
P
B
P
A
2018
2017
. Tính thể tích V của khối tứ diện PMNC. A.
27.
2
12
B.
9.2018....
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M, N lần lượt là trung điểm các cạnh AD, BD. Gọi P là điểm trên cạnh AB sao cho P B P A = 2018 2017 . Tính thể tích V của khối tứ diện PMNC.
A. 27. 2 12
B. 9.2018. 2 16.2017
C. 9. 2 16
D. 9.2017. 2 16.2018
Cho khối tứ diện ABCD có thể tích là V. Gọi E, F, G lần lượt là trung điểm BC, BD, CD và M, N, P, Q lần lượt là trọng tâm
∆
A
B
C
;
∆
A
B
D
;
∆
A
C
D
;
∆
B
C
D
. Tính thể tích khối tứ diện MNPQ theo V. A.
V
9
B.
V
3
C. ...
Đọc tiếp
Cho khối tứ diện ABCD có thể tích là V. Gọi E, F, G lần lượt là trung điểm BC, BD, CD và M, N, P, Q lần lượt là trọng tâm ∆ A B C ; ∆ A B D ; ∆ A C D ; ∆ B C D . Tính thể tích khối tứ diện MNPQ theo V.
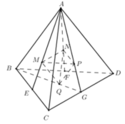
A. V 9
B. V 3
C. 2 V 9
D. V 27
Cho hình chóp S.ABC có
S
A
S
B
S
C
3
,
tam giác ABC vuông cân tại B và
A
C
2
2
. Gọi M, N lần lượt là trung điểm của AC và BC. Trên hai cạnh SA, SB lấy các điểm P, Q tương ứng sao cho
S
P
1
,
S
Q
2.
Tính thể tích V của khối tứ diện...
Đọc tiếp
Cho hình chóp S.ABC có S A = S B = S C = 3 , tam giác ABC vuông cân tại B và
A C = 2 2 . Gọi M, N lần lượt là trung điểm của AC và BC. Trên hai cạnh SA, SB lấy các điểm P, Q tương ứng sao cho S P = 1 , S Q = 2. Tính thể tích V của khối tứ diện M N P Q .
A. V = 7 18
B. V = 3 12
C. V = 34 12
D. V = 34 144
Cho hình chóp .S ABCD có đáy ABCD là hình bình hành. Hai điểm M, N thuộc các cạnh AB và AD (M, N không trùng với A, B, D). sao cho
A
B
A
M
+
2.
A
D
A
N
4.
Kí hiệu V,
V
1
lần lượt là thể tích của các khối chóp...
Đọc tiếp
Cho hình chóp .S ABCD có đáy ABCD là hình bình hành. Hai điểm M, N thuộc các cạnh AB và AD (M, N không trùng với A, B, D). sao cho A B A M + 2. A D A N = 4. Kí hiệu V, V 1 lần lượt là thể tích của các khối chóp S . A B C D v à S . M B C D N . Tìm giá trị lớn nhất của V 1 V
A. 2 3
B. 3 4
C. 1 6
D. 14 17
Trong không gian Oxyz, cho tứ diện ABCD có A (1;1;1), B (2;0;2), C ( -1;-1;0) và D ( 0;3;4). Trên các cạnh AB , AC, AD lần lượt lấy các điểm B, C, D sao cho thể tích của khối tứ diện ABCD nhỏ nhất và
A
B
A
B
+
A
C
A
C
+
A...
Đọc tiếp
Trong không gian Oxyz, cho tứ diện ABCD có A (1;1;1), B (2;0;2), C ( -1;-1;0) và D ( 0;3;4). Trên các cạnh AB , AC, AD lần lượt lấy các điểm B', C', D' sao cho thể tích của khối tứ diện AB'C'D' nhỏ nhất và A B A B ' + A C A C ' + A D A D ' = 4 . Tìm phương trình của mặt phẳng (B’C’D’)
A. 16 x + 40 y - 44 z + 39 = 0
B. 16 x - 40 y - 44 z + 39 = 0
C. 16 x + 40 y + 44 z + 39 = 0
D. 16 x + 40 y - 44 z - 39 = 0




