Các câu hỏi tương tự
Trong không gian cho hình thang cân ABCD có AB//CD, ABa, CD2a, ADa. Gọi M, N lần lượt là trung điểm của AB và CD. Gọi K là khối tròn xoay được tạo ra khi xoay hình thang ABCD quanh trục MN. Tính thể tích V của khối K. A.
V
5
πa
3
3
8
B.
V
5
πa
3...
Đọc tiếp
Trong không gian cho hình thang cân ABCD có AB//CD, AB=a, CD=2a, AD=a. Gọi M, N lần lượt là trung điểm của AB và CD. Gọi K là khối tròn xoay được tạo ra khi xoay hình thang ABCD quanh trục MN. Tính thể tích V của khối K.
A. V = 5 πa 3 3 8
B. V = 5 πa 3 3 16
C. V = 7 πa 3 3 12
D. V = 7 πa 3 3 12
Trong không gian, cho hình thang cân ABCD có AB//CD,
A
B
a
,
C
D
2
a
,
A
D
a
. Gọi M, N lần lượt là trung điểm của AB. CD. Gọi K là khối tròn xoay được tạo ra khi quay hình thành ABCD quanh trục MN. Tính diện tích toàn phần
S
φ
của khối K. A.
S
φ...
Đọc tiếp
Trong không gian, cho hình thang cân ABCD có AB//CD, A B = a , C D = 2 a , A D = a . Gọi M, N lần lượt là trung điểm của AB. CD. Gọi K là khối tròn xoay được tạo ra khi quay hình thành ABCD quanh trục MN. Tính diện tích toàn phần S φ của khối K.
A. S φ = 9 π a 2 4
B. S φ = 17 π a 2 4
C. S φ = 7 π a 2 4
D. S φ = 11 π a 2 4
Trong không gian, cho hình thang cân ABCD có AB//CD, AB a, CD 2a, AD a. Gọi M, N lần lượt là trung điểm của AB, CD. Gọi K là khối tròn xoay được tạo ra khi quay hình thang ABCD quanh trục MN. Tính diệc tích xung quanh
S
x
q
của khối K A.
S
x
q
πa
2
2
B. ...
Đọc tiếp
Trong không gian, cho hình thang cân ABCD có AB//CD, AB = a, CD = 2a, AD = a. Gọi M, N lần lượt là trung điểm của AB, CD. Gọi K là khối tròn xoay được tạo ra khi quay hình thang ABCD quanh trục MN. Tính diệc tích xung quanh S x q của khối K
A. S x q = πa 2 2
B. S x q = 3 πa 2 2
C. S x q = 3 πa 2
D. S x q = πa 2
Cho hình chóp S.ABCD có đáy ABCD là hình thoi và có thể tích bằng 2. Gọi M, N lần lượt là các điểm trên cạnh SB và SD sao cho
S
M
S
B
S
N
S
D
k
. Tìm giá trị của k để thể tích khối chóp S.AMN bằng
1
8
A.
k...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi và có thể tích bằng 2. Gọi M, N lần lượt là các điểm trên cạnh SB và SD sao cho S M S B = S N S D = k . Tìm giá trị của k để thể tích khối chóp S.AMN bằng 1 8
A. k = 1 8
B. k = 2 2
C. k = 2 4
D. k = 1 4
Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AC và BC. Trên BD lấy điểm K sao cho BK 2KD. Gọi E là giao điểm của JK và CD; F là giao điểm của IE và AD. Tìm giao điểm của AD và (IJK). A. Điểm I B. Điểm E C. Điểm F D. Điểm K
Đọc tiếp
Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AC và BC. Trên BD lấy điểm K sao cho BK = 2KD. Gọi E là giao điểm của JK và CD; F là giao điểm của IE và AD. Tìm giao điểm của AD và (IJK).
A. Điểm I
B. Điểm E
C. Điểm F
D. Điểm K
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a với
S
A
a
2
,
S
B
a
3
2
,
B
A
D
^
60
°
và mặt phẳng (SAB) vuông góc với mặt phẳng đáy. Gọi H, K lần lượt là trung điểm của AB,BC Thể tích tứ diện K.SDC có giá trị là: A.
V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a với S A = a 2 , S B = a 3 2 , B A D ^ = 60 ° và mặt phẳng (SAB) vuông góc với mặt phẳng đáy. Gọi H, K lần lượt là trung điểm của AB,BC Thể tích tứ diện K.SDC có giá trị là:
A. V = a 3 4
B. V = a 3 16
C. V = a 3 8
D. V = a 3 32
Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k 2 và phép đối xứng tâm I biến tứ giác IGHF thành A. AIFD B. BCFI C. CIEB D. DIEA
Đọc tiếp
Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm I biến tứ giác IGHF thành
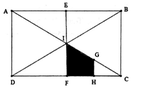
A. AIFD
B. BCFI
C. CIEB
D. DIEA
Cho tứ diện ABCD, gọi I,J,K lần lượt là trung điểm của AB,BC,BD. Giao tuyến của hai mặt phẳng (ABD) và (IJK) là: A. Đường thẳng qua J song song với AC B. Đường thẳng qua J song song với CD C. Đường thẳng qua K song song với AB D. Đường thẳng qua I song song với AD
Đọc tiếp
Cho tứ diện ABCD, gọi I,J,K lần lượt là trung điểm của AB,BC,BD. Giao tuyến của hai mặt phẳng (ABD) và (IJK) là:
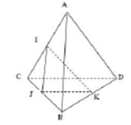
A. Đường thẳng qua J song song với AC
B. Đường thẳng qua J song song với CD
C. Đường thẳng qua K song song với AB
D. Đường thẳng qua I song song với AD
Cho hình lập phương a 1 có cạnh bằng a 1. Một đường thẳng d đi qua đỉnh D và tâm I cuả mặt bên BCCB. Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng (BCCB) và (ABCD) sao cho trung điểm K của MN thuộc đường thẳng d ( tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là: A. a 1 B. a
1
2
C.
a
2
5
D.
a...
Đọc tiếp
Cho hình lập phương a = 1 có cạnh bằng a = 1. Một đường thẳng d đi qua đỉnh D ' và tâm I cuả mặt bên BCC'B'. Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng (BCC'B') và (ABCD) sao cho trung điểm K của MN thuộc đường thẳng d ( tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là:
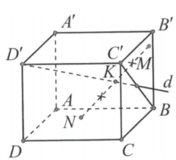
A. a =1
B. a = 1 2
C. a = 2 5
D. a = 1 3



