Các câu hỏi tương tự
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng:
G
D
→
.
G
A
→
+
G
D
→
.
G
B
→
+
G
D...
Đọc tiếp
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng: G D → . G A → + G D → . G B → + G D → . G C → = 0
Cho tứ diện ABCD. Gọi M,N,P lần lượt là trung điểm của các cạnh BC, BD,CD.
a. Xác định giao tuyến của hai mặt phẳng (AMN) và (ACD).
b. Chứng minh rằng đường thẳng BC song song với mặt phẳng (ANP)
c. Gọi G, H lần lượt là trọng tâm của tam giác ABC và ACD. Chứng minh GH // BD.
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M và M’ lần lượt là trung điểm của các cạnh BC và B’C’.a) Chứng minh rằng AM song song với A’M’.b) Tìm giao điểm của mặt phẳng (A’B’C’) với đường thẳng A’M.c) Tìm giao tuyến d của hai mặt phẳng (AB’C’) và (BA’C’).d) Tìm giao điểm G của đường thẳng d với mp(AMA’). Chứng minh G là trọng tâm của tam giác AB’C’.
Đọc tiếp
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M và M’ lần lượt là trung điểm của các cạnh BC và B’C’.
a) Chứng minh rằng AM song song với A’M’.
b) Tìm giao điểm của mặt phẳng (A’B’C’) với đường thẳng A’M.
c) Tìm giao tuyến d của hai mặt phẳng (AB’C’) và (BA’C’).
d) Tìm giao điểm G của đường thẳng d với mp(AMA’). Chứng minh G là trọng tâm của tam giác AB’C’.
Cho tứ diện đều ABCD có cạnh a. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BGG’) là: A. B. C. D.
Đọc tiếp
Cho tứ diện đều ABCD có cạnh a. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BGG’) là:
A. ![]()
B. ![]()
C. ![]()
D. 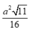
Cho hình thang ABCD có AB // CD và AB 2a, BC CD DA a. Đường thẳng d vuông góc với mặt phẳng (ABCD) tại A. Gọi S là một điểm duy nhất thay đổi trên d. (P) là một mặt phẳng qua A vuông góc với SB tại I và cắt SC, SD lần lượt tại J, K.a) Chứng minh tứ giác BCJI, AIJK là các tứ giác nội tiếp.b) Gọi O là trung điểm của AB, O là tâm đường tròn ngoại tiếp tứ giác BCJI. Chứng minh rằng OO ⊥ (SBC).c) Chứng minh rằng khi S thay đổi trên d thì JK luôn luôn đi qua một điểm cố định.d) Tìm một điểm cách đ...
Đọc tiếp
Cho hình thang ABCD có AB // CD và AB = 2a, BC = CD = DA = a. Đường thẳng d vuông góc với mặt phẳng (ABCD) tại A. Gọi S là một điểm duy nhất thay đổi trên d. (P) là một mặt phẳng qua A vuông góc với SB tại I và cắt SC, SD lần lượt tại J, K.
a) Chứng minh tứ giác BCJI, AIJK là các tứ giác nội tiếp.
b) Gọi O là trung điểm của AB, O' là tâm đường tròn ngoại tiếp tứ giác BCJI. Chứng minh rằng OO' ⊥ (SBC).
c) Chứng minh rằng khi S thay đổi trên d thì JK luôn luôn đi qua một điểm cố định.
d) Tìm một điểm cách đều các điểm A, B, C, D, I, J, K và tìm khoảng cách đó.
e) Gọi M là giao điểm của JK và (ABCD). Chứng minh rằng AM là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
f) Khi S thay đổi trên d, các điểm I, J, K lần lượt chạy trên đường nào.
Cho tứ diện ABCD. Gọi
G
1
,
G
2
,
G
3
lần lượt là trọng tâm các tam giác ABC, ACD, ABD. Chứng minh rằng
(
G
1
G
2
G
3
)
/
/
(
B
C
D
)
.
Đọc tiếp
Cho tứ diện ABCD. Gọi G 1 , G 2 , G 3 lần lượt là trọng tâm các tam giác ABC, ACD, ABD. Chứng minh rằng ( G 1 G 2 G 3 ) / / ( B C D ) .
Cho tứ diện ABCD cạnh a. Gọi G là trọng tâm của tam giác ABC. Qua G dựng một mặt phẳng (P) song song với mặt phẳng (P) song song với mặt phẳng (BCD). Tìm diện tích thiết diện của (P) và tứ diện ABCD. A.
a
2
3
4
B.
a
2
3
9
C. ...
Đọc tiếp
Cho tứ diện ABCD cạnh a. Gọi G là trọng tâm của tam giác ABC. Qua G dựng một mặt phẳng (P) song song với mặt phẳng (P) song song với mặt phẳng (BCD). Tìm diện tích thiết diện của (P) và tứ diện ABCD.
A. a 2 3 4
B. a 2 3 9
C. a 2 2 16
D. a 2 3 18
Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Mặt phẳng (GCD) cắt tứ diện theo 1 thiết diện có diện tích là A.
a
2
3
2
.
B.
a
2
2
4
.
C.
a
2...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Mặt phẳng (GCD) cắt tứ diện theo 1 thiết diện có diện tích là
A. a 2 3 2 .
B. a 2 2 4 .
C. a 2 2 6 .
D. a 2 4 4 .
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn. Gọi M là trung điểm của đoạn AB, E là giao điểm của hai cạnh của hình thang ABCD và G là trọng tâm của tam giác ECD.(a) Chứng minh rằng bốn điểm S, E, M, G cùng thuộc một mặt phẳng (α) và mặt phẳng này cắt cả hai mặt phẳng (SAC) và (SBD) theo cùng một giao tuyến d.(b) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBC).(c) Lấy một điểm K trên đoạn SE và gọi C SC ∩KB, DSD ∩KA. Chứng minh rằng hai giao điểm của AC và BD thuộc đườn...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn. Gọi M là trung điểm của đoạn AB, E là giao điểm của hai cạnh của hình thang ABCD và G là trọng tâm của tam giác ECD.
(a) Chứng minh rằng bốn điểm S, E, M, G cùng thuộc một mặt phẳng (α) và mặt phẳng này cắt cả hai mặt phẳng (SAC) và (SBD) theo cùng một giao tuyến d.
(b) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBC).
(c) Lấy một điểm K trên đoạn SE và gọi C' = SC ∩KB, D'=SD ∩KA. Chứng minh rằng hai giao điểm của AC' và BD' thuộc đường thẳng d nói trên.





