Cho tứ diện ABCD có O là trung điểm của đoạn thẳng nối trung điểm của hai cạnh đối diện và a là số thực dương không đổi. Tập hợp các điểm M trong không gian thỏa mãn hệ thức M A → + M B → + M C → + M D → = a là
A. mặt cầu tâm O bán kính r = a 3 .
B. mặt cầu tâm O bán kính r = a 4 .
C. mặt cầu tâm O bán kính r = a .
D. mặt cầu tâm O bán kính r = a 2 .
Đáp án B
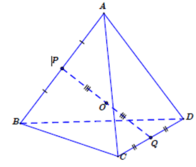
* Gọi P, Q lần lượt là trung điểm của AB, CD. Theo giả thiết O là trung điểm của PQ nên suy ra O là trọng tâm của tứ diện ABCD.
M A → + M B → + M C → + M D → = a
⇔ 4 O M → = a ⇔ O M = a 4
Vậy tập hợp các điểm M trong không gian là mặt cầu tâm O bán kính r = a 4



