Đáp án D
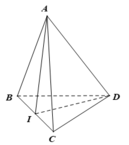
Gọi I là trung điểm của BC.
Vì ∆ ABC cân tại A nên AI ⊥ BC (1)
Vì ∆ DBC cân tại D nên DI ⊥ BC (2)
Từ (1) và (2) suy ra BC ⊥ (AID) => BC AD
Đáp án D

Gọi I là trung điểm của BC.
Vì ∆ ABC cân tại A nên AI ⊥ BC (1)
Vì ∆ DBC cân tại D nên DI ⊥ BC (2)
Từ (1) và (2) suy ra BC ⊥ (AID) => BC AD
Cho tứ diện ABCD có AB=AC và DB=DC. Khẳng định nào sau đây đúng?
A. A B ⊥ A B C
B. A C ⊥ B C
C. C D ⊥ A B D
D. B C ⊥ A D
Cho tứ diện ABCD có AB = AC và DB = DC. Khẳng định nào sau đây đúng?
A. A B ⊥ A B C
B. A C ⊥ B D
C. C D ⊥ A B D
D. B C ⊥ A D
Cho tứ diện ABCD có AB = AC và DB = DC. Khẳng định nào sau đây đúng?
A. AB ⊥ (ABC)
B. AC ⊥ BD
C. BC ⊥ AD
D. CD ⊥ (ABD)
Cho tứ diện ABCD có AB=AC=2, DB=DC=3. Khẳng định nào sau đây đúng?
A. B C ⊥ A D
B. A C ⊥ B D
C. A B ⊥ B C D
D. D C ⊥ A B C
Cho tứ diện ABCD có AB=AC=2, DB=DC=3 Khẳng định nào sau đây đúng?
![]()
![]()
![]()
![]()
Cho tứ diện ABCD. Gọi M và P lần lượt là trung điểm của AB và CD. Đặt A B → = b → ; A C → = c → ; A D → = d . Khẳng định nào sau đây đúng?
![]()
![]()
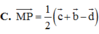
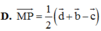
Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai?
A. Góc giữa hai mặt phẳng (ABC) và (ABD) là C B D ^
B. Góc giữa hai mặt phẳng (ACD) và (BCD) là A I B ^
C. (BCD) ⊥ (AIB).
D. (ACD) ⊥ (AIB).
Cho tứ diện ABCD có AB = 2, AC =3, AD =BC = 4, B D = 2 5 , CD = 5. Khoảng cách giữa hai đường thẳng AC và BD gần nhất với giá trị nào sau đây.
A. 4
B. 1
C. 2
D. 3
Cho tứ diện ABCD có cạnh AB, BC, BD bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?
A. Góc giữa AC và (BCD) là góc ACB.
B. Góc giữa AD và (ABC) là góc ADB.
C. Góc giữa AC và (ABD) là góc CAB.
D. Góc giữa CD và (ABD) là góc CBD.