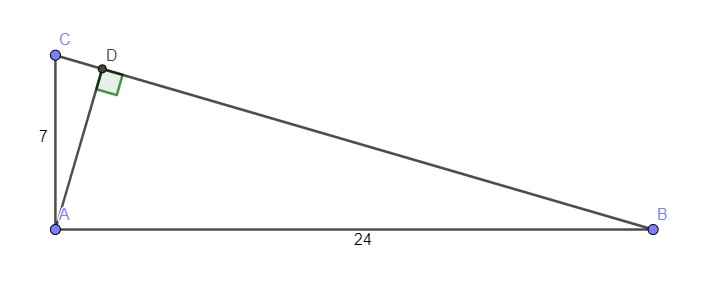
Giả sử tam giác ABC vuông tại A với \(AB=24\) ; \(AC=7\)
Kẻ đường cao AD ứng với cạnh huyền
Ta có: \(BC=\sqrt{AB^2+AC^2}=25\)
Áp dụng hệ thức lượng:
\(AC^2=CD.BC\Rightarrow CD=\dfrac{AC^2}{BC}=1,96\)
\(\Rightarrow BD=BC-CD=23,04\)
Áp dụng hệ thức lượng: \(AD^2=BD.CD\Rightarrow AD=\sqrt{BD.CD}=6,72\)
\(S_{ACD}=\dfrac{1}{2}AD.CD=6,5856\)
\(S_{ABD}=\dfrac{1}{2}AD.BD=77,4144\)
Cho tam giác vuông với các cạnh góc vuông là 7 và 24. Kẻ đường cao ứng với cạnh huyền. Tính diện tích hai tam giác vuông tạo thành
cho tam giác vuông với các cạnh góc vuông là 7 và 24. Kẻ đường cao ứng với cạnh góc huyền. Tính diện tích 2 tam giác vuông tạo thành
cho tam giác vuông với các cạnh góc vuông là 7 và 24. Kẻ đường cao ứng với cạnh huyền. Tính độ dài đường cao và các đoạn thẳng mà đương cao đó chia ra trên cạnh huyền
giúp tui với
Cho tam giác vuông với các cạnh góc vuông có độ dài là 5 và 7, kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và các đoạn thẳng mà nó chia ra trên cạnh huyền.
Cho 1 tam giác vuông có cách cạnh góc vuông lần lượt là 7cm và 24 cm kẻ đường cao tương ứng với cạnh huyền. Tính độ dài đường cao và các đoạn thẳng mà đường cao đó chia ra trên cạnh huyền
Cho tam giác MNP vuông tại M , kẻ đường cao MH.Biết hai hình chiếu của hai cạnh góc vuông là 7 và 12.Tính các cạnh của tam giác vuông đó.
1) Một tam giác vuông có canh huyền là 5 và đường cao ứng với cạnh huyền là 2. Hãy tính cạnh nhỏ nhất của tam giác vuông này.
2) Cho một tam giác vuông. Biết tỉ số hai cạnh góc vuông là 3:4 và cạnh huyền là 125 cm. Tính độ dài các cạnh góc vuông và hình chiếu của các cạnh góc vuông trên cạnh huyền.
cho tam giác vuông có độ dài các cạnh góc vuông là 5cm và 12 cm tính các cạnh các góc đường cao vàtrung tuyến ứng với cạnh huyền của tam giác vuông đó
cho tam giác vuông với các cạnh góc vuông lần lượt là 5cm và 7cm, kẻ đường cao tương ứng với cạnh huyền. hãy tính đường cao này và các đoạn thẩng mà nó đỉnh trên cạnh huyền
