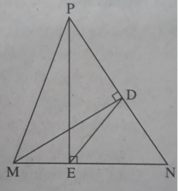
Hai tam giác vuông DMN và EPN đồng dạng vì có góc nhọn N chung nên D N M N = E N P N Hai tam giác DNE và MNP đồng dạng vì có góc N chung và D N M N = E N P N

Hai tam giác vuông DMN và EPN đồng dạng vì có góc nhọn N chung nên D N M N = E N P N Hai tam giác DNE và MNP đồng dạng vì có góc N chung và D N M N = E N P N
Cho tam giác nhọn MNP. Gọi D là chân đường cao của tam giác đo kẻ từ M. Chứng minh rằng D P = M N . sin N t g P
Cho tam giác nhọn MNP. Gọi D là chân đường cao của tam giác đo kẻ từ M. Chứng minh rằng S M N P = 1 2 . M P . N P . sin P
Cho tam giác MNP có 3 góc nhọn , MN < MP . Gọi I là trung điểm của NP , H,K lần lượt là chân đường cao của tam giác MNP kẻ từ N và P; O là trực tâm. L là giao điểm của HK và NP. Chứng minh : LO vuông góc với MI.
Cho tam giác MNP vuông tại M đường cao MH. Biết NH=4cm, HP=16cm.
a) Tính MN, MP và MH.
b) Gọi D, E là chân đường phân giác kẻ từ H lên AB, AC. Chứng minh: AD.AB=AE.AC.
c) Biết AD=5cm. Tính diện tích hình chữ nhật ADHE
Cho tam giác MNP vuông tại m có MN = 3 cm góc b = 37 độ A giải tam giác vuông MNP ( số đo góc làm tròn đến độ) B: kẻ đường cao MH ( H€NP ) TÍNH MH Chứng minh góc nmh bằng góc P từ đó tính các tỉ số lượng góc của góc NMH
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Gọi D,E,K lần lượt là chân đường cao kẻ từ A,B,C của tam giác ABC . H là trực tâm của tam giác ABC
a,CM: tứ giác HDCE nội tiếp
b, Gọi M là giao điểm của AH và (O). Chứng minh D là trung điểm của HM
c,Chứng minh: OA vuông góc với EK
Bài 4: Cho tam giác ABC có ba góc nhọn và đường cao BE. Gọi H và K lần lượt là chân các đường vuông góc kẻ từ điểm E đến các đường thẳng AB và BC.
1) Chứng minh tứ giác BHEK là tứ giác nội tiếp
2) Chứng minh BH.BA = BK.BC
3) Gọi F là chân đường vuông góc kẻ từ điểm C đến đường thẳng AB và I là trung điểm của đoạn thẳng EF. Chứng minh ba điểm H, I, K là ba điểm thẳng hàng.
Cho tam giác nhọn ABC nội tiếp đường tròn O. Gọi D,E,Flần lượt là chân các đường cao kẻ từ ba đỉnh A,B,C của tam giác. Đường thẳng EF cắt đường tròn O tại M (M khác phía với O so với đường thẳng AB). Đường thẳng BM cắt đường thẳng DF tại N. Chứng minh rằng AM=AN
cho tam giác mnp,có mn=8cm,mp=6cm,pn=10cm,đường cao mh.gọi e và f là chân đường vuông góc từ h lên mn,mp.chứng minh mh^3=np.ne.pe