Chọn đáp án D.
* Chứng minh tứ giác ADHE nội tiếp trong một đường tròn.

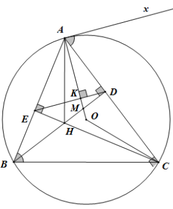
Trong nửa mặt phẳng bờ AC không chứa điểm B, vẽ tia tiếp tuyến Ax với đường tròn (O)

Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Chọn đáp án D.

* Chứng minh tứ giác ADHE nội tiếp trong một đường tròn.

Trong nửa mặt phẳng bờ AC không chứa điểm B, vẽ tia tiếp tuyến Ax với đường tròn (O)

Cho tam giác ABC nhọn nội tiếp đường tròn ( O , R) . Gọi H là giao của hai đường cao BD CE của tam giác ABC.
Chứng minh
a Tứ giác ADHE nội tiếp
b Đường thăng AO cắt BD ED lần lượt tại K và M . Chứng minh AK nhân AM bằng AD^ 2
cho tam giác ABC nhọn , AB<AC nội tiếp đường tròn (O). Các đường cao BD và CE của tam giác ABC cắt nhau tại H. Gọi K là giao điểm của DE và CB.
a)CMR: Tứ giác BCDE nội tiếp
b) C/m : KB.KC=KE.KD
c) Gọi M là trung điểm của BC , AK cắt đường tròn (O) tại điểm thứ 2 N . C/m : 3 điểm M,H,N thẳng hàng
Cho tam giác ABC nội tiếp trong đường tròn (O), kẻ các đường cao BD và CE của tam giác ABC chúng cắt nhau tại H a) Chứng minh tứ giác ADHE nội tiếp . b) Gọi M, N là giao điểm của DE với đường tròn, xy là tiếp tuyến của đường tròn (O) tại A. Chứng minh: MN//xy.
. Cho tam giác ABC nhọn (AB< AC ), đường tròn tâm O đường kính BC cắtAB tại E ,AC tại D . GọiH là giao điểm của BD và CE , S là giao điểm của đường thẳng BC và ED .
a) Chứng minh tứ giác ADHE nội tiếp và AH vuông góc với BC
. b) Gọi I là giao điểm của AH và BC . Chứng minh BIHE nội tiếp và góc EID = GOC EOD
c) Gọi K là giao điểm của AS với đường tròn ngoại tiếp tam giácADE . Chứng minh O H K thẳng hàng
Cho tam giác ABC (AB < AC) có ba góc nhọn nội tiếp đường tròn tâm O. Gọi BD, CE là hai đường cao, H là trực tâm.
a) Chứng minh: ADHE, BEDC nội tiếp được.
b) Chứng minh: HB.HD=HE.HC
c) Các đường thẳng BD, CE cắt (O) lần lượt tại I và K. Chứng minh AC là đường trung trực của của HI.
d) Chứng minh: A là tâm đường tròn ngoại tiếp tam giác HIK.
Cho tam giác ABC nhọn (AB<AC) nội tiếp đường tròn (O). Vẽ các đường cao BD,CE của tam giác ABC (D thuộc AC, E thuộc AB).
a) Chứng minh tứ giác BCDE nội tiếp đường tròn.
b) Gọi giao điểm của AO với BD và ED lần lượt tại K, M.
Chứng minh: \(\frac{1}{MD^2}=\frac{1}{KD^2}+\frac{1}{AD^2}\)
Bài 1: Cho tam giác ABC (AB < AC ) có 3 góc nhọn. Đường tròn tâm O đường kính BC cắt các cạnh AC, AB lần lượt tại D, E. Gọi H là giao điểm của BD và CE; F là giao điểm của AH và BC
a) CM: Tứ giác AEHD nội tiếp đường tròn
b) Gọi M là trung điểm của AH. CM: MD là tiếp tuyến của đg tròn (O)
c) Gọi K là giao điểm của AH và DE. CM: MD2 = MK.MF và K là trực tâm của tam giác MBC
d) CM: 2/FK = 1/FH + 1/FA
Cho tam giác nhọn ABC (AB < AC). Đường tròn tâm O đường kính BC cắt AB và AC lần lượt tại E và D. Gọi H là giao điểm của BD và CE; AH cắt BC tại I.
c) Chứng minh tứ giác OIED nội tiếp.
Cho tam giác ABC nhọn đường tròn O đường kính BC cắt AB, AC lần lượt tại E và D,CE cắt BD tại H a) CM tứ giác ADHE nội tiếp b) AH cắt BC tại F. CM FA là tia p/giác góc DFE c) EF cắt đường tròn tại K. CM DK//AF d) cho bt góc BCD=45° ,BC=4 .Tín diện tích tam giác ABC