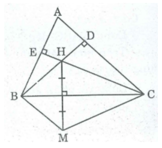
Gọi giao điểm BH với AC là D, giao điểm của CH và AB là E, H là trực tâm của ΔABC
⇒ BD ⊥ AC, CE ⊥ AB
Xét tứ giác ADHE, ta có:
∠ (DHE) = 360 0 – ( ∠ A + ∠ D + ∠ E ) = 360 0 - 60 0 + 90 0 + 90 0 = 120 0
∠ (BHC) = ∠ (DHE)(đối đỉnh)
∆ BHC = ∆ BMC (chứng minh trên)
⇒ ∠ (BMC) = ∠ (BHC)
Suy ra: ∠ (BMC) = ∠ (DHE) = 120 0
cho tam giác nhọn ABC có góc A = 60 độ , trực tâm H. Gọi M là điểm đối xứng với H qua BC
a) Cm: tam giác BHC= tam giác BMC
b) tính góc BMC
Cho tam giác ABC có góc A= 60 độ, trực tâm H . Gọi M là điểm đối xứng với H qua BC
a, C/M tam giác BHC = tam giác BMC
b, Tính BMC
cho tam giác abc nhọn có góc a bằng 40 độ trực tâm h gọi m là điểm đối xứng với h qua bc. tính góc bmc
Cho tam giác nhọn ABC có gốc A=60 độ , trực tâm H .Gọi M là điểm đối xứng với H qua BC
a, Chứng minh tam giác BHC=tam giác BMC
b, Tính gốc BMC
Cho tam giác nhọn ABC,có góc A=60o ,trực tâm H.Gọi M là điểm đối xứng với H qua BC
a)Chứng minh tam giác BHC=BMC
b) Tính góc BMC
Cho tam giác ABC, có A ^ = 60°, trực tâm H. Gọi M là điểm đối xứng với H qua BC.
a) Chứng minh ∆BHC = ∆BMC.
b) Tính B M C ^
Cho tam giác nhọn ABC có góc A=60o, trực tâm H. Gọi M là điểm đối xứng với H qua BC
a) chứng minh ΔBHC=ΔBMC
b) Tính góc BMC
Cho tam giác nhọn ABC có ∠ A = 60 0 , trực tâm H. Gọi M là điểm đối xứng với H qua BC. Chứng minh ∆ BHC = ∆ BMC
B1) cho tam giác ABC có A^=70 độ, điểm M thuộc cạnh BC.Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC
a) c/m AD=AE
b) tính góc DAE
B2) cho tam giác nhọn có A^=60 độ, trực tâm H. Gọi M là điểm đối xứng với H qua BC
a)c/m tam giác BHC =tam giácBMC
b) tính góc BMC
B3)cho hình thang vuông ABCD ( A^=90, D^=90 độ ) . H là điểm đối xứng với B qua AD , I là giao điểm của CH và AD . c/m góc AIB = góc DIC
ai giúp với..
