Các câu hỏi tương tự
Cho tam giác đều ABC, O là trung điểm của BC. Trên các cạnh AB, AC lần lượt lấy các điểm di động D và E sao cho góc DOE 60o.a) Chứng minh tích BD.CE không đổi.b) Chứng minh ΔBOD ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.c) Vẽ đường tròn tâm O tiếp xúc với AB. Chứng minh rằng đường tròn này luôn tiếp xúc với DE.
Đọc tiếp
Cho tam giác đều ABC, O là trung điểm của BC. Trên các cạnh AB, AC lần lượt lấy các điểm di động D và E sao cho góc DOE = 60o.
a) Chứng minh tích BD.CE không đổi.
b) Chứng minh ΔBOD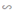 
ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.
c) Vẽ đường tròn tâm O tiếp xúc với AB. Chứng minh rằng đường tròn này luôn tiếp xúc với DE.
Cho tam giác đều ABC, O là trung điểm của BC. Trên các cạnh AB, AC lần lượt lấy các điểm di động D và E sao cho góc DOE
60
o
.a) Chứng minh tích BD.CE không đổi.b) Chứng minh ΔBOD ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.c) Vẽ đường tròn tâm O tiếp xúc với AB. Chứng minh rằng đường tròn này luôn tiếp xúc với DE.
Đọc tiếp
Cho tam giác đều ABC, O là trung điểm của BC. Trên các cạnh AB, AC lần lượt lấy các điểm di động D và E sao cho góc DOE = 60 o .
a) Chứng minh tích BD.CE không đổi.
b) Chứng minh ΔBOD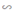 
ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.
c) Vẽ đường tròn tâm O tiếp xúc với AB. Chứng minh rằng đường tròn này luôn tiếp xúc với DE.
Cho tam giác đều ABC , O là trung điểm của BC. Lấy D, E thuộc AB , AC sao cho góc DOE = 60 độ
a. Chứng minh tích BD.CE không đổi
b.Tam giác BOD đồng dạng với tam giác OED, OD là phân giác góc BDE
c.Vẽ đường trờn tâm O tiếp xúc với AB . Chứng minh đường tròn này tiếp xúc với DE
cho tam giác đều abc,o là trung điểm của bc.trên các cạnh ab,ac lần lượt lấy các điểm di động d và e sao cho góc doe=60 độ
a/ chứng minh tích bd.ce không đổi
b/ chứng minh tam giác bod đồng dạng với tam giác oed
Bài 1: Cho đường tròn tâm (O) dây AB cố định ( O không thuộc AB). P là điểm di động trên AB(P khác A và B). Qua A, P vẽ đường tròn tâm C tiếp xúc với đường tròn tâm (O) tại A. Qua B,P vẽ đường tròn tâm D tiếp xúc với đường tròn (O) tại B. Hai đường tròn (C) và (D) cắt nhau tại N (khác P).a) Chứng minh góc ANP góc BNP b) Chứng minh góc PNO 90 độBài 2: Cho tam giác ABC có goác A 60 độ, ABAC. Trên cạnh AC lấy điểm E sao cho CEAB. Gọi P, Q lần lượt là trung điểm của BC, AE. Tính góc AQP
Đọc tiếp
Bài 1: Cho đường tròn tâm (O) dây AB cố định ( O không thuộc AB). P là điểm di động trên AB(P khác A và B). Qua A, P vẽ đường tròn tâm C tiếp xúc với đường tròn tâm (O) tại A. Qua B,P vẽ đường tròn tâm D tiếp xúc với đường tròn (O) tại B. Hai đường tròn (C) và (D) cắt nhau tại N (khác P).
a) Chứng minh góc ANP = góc BNP
b) Chứng minh góc PNO = 90 độ
Bài 2: Cho tam giác ABC có goác A= 60 độ, AB<AC. Trên cạnh AC lấy điểm E sao cho CE=AB. Gọi P, Q lần lượt là trung điểm của BC, AE. Tính góc AQP
cho tam giác ABC , Đường tròn (I) nội tiếp tam giác tiếp xúc với cạnh BC tại D. Đường tròn (K) là đường tròn bàng tiếp trong góc A tiếp xúc với BC tại E. Gọi F là điểm đối xứng của D qua I. Chứng minh rằng
a) tam giác AIF đồng dạng với tam giác AKE
b) trung điểm của BC cũng là trung điểm của DE
Cho đường tròn tâm O có đường kính AB R2 . Gọi M là điểm di động trên đường tròn O . Điểm M khác AB, ; dựng đường tròn tâm M tiếp xúc với AB tại H . Từ A và B kẻ hai tiếp tuyến AC và BD với đường tròn tâm M vừa dựng. a) Chứng minh BM AM , lần lượt là các tia phân giác của các góc ABD và BAC .b) Chứng minh ba điểm C M D , , nằm trên tiếp tuyến của đường tròn tâm O tại điểm M .c) Chứng minh AC BD không đổi, từ đó tính tích AC BD. theo CD .d) Giả sử ngoài AB, trên nửa đường tròn đường kính AB không...
Đọc tiếp
Cho đường tròn tâm O có đường kính AB R2 . Gọi M là điểm di động trên đường tròn O . Điểm M khác AB, ; dựng đường tròn tâm M tiếp xúc với AB tại H . Từ A và B kẻ hai tiếp tuyến AC và BD với đường tròn tâm M vừa dựng.
a) Chứng minh BM AM , lần lượt là các tia phân giác của các góc ABD và BAC .
b) Chứng minh ba điểm C M D , , nằm trên tiếp tuyến của đường tròn tâm O tại điểm M .
c) Chứng minh AC BD không đổi, từ đó tính tích AC BD. theo CD .
d) Giả sử ngoài AB, trên nửa đường tròn đường kính AB không chứa M có một điểm N cố định. gọi I là trung điểm của MN , kẻ IP vuông góc với MB . Khi M chuyển động thì P chuyển động trên đường cố định nào.
Cần giải câu d
Cho đoạn thẳng AB với trung điểm O. Trên nửa mặt phẳng bờ AB kẻ các tia Ax, By vuông góc vớiAB. Một góc vuông POQ quay xung quanh O cắt Ax, By tại P, Q. Gọi P’ là giao điểm của các tia đốicủa các tia OP, By.a) Tam giác QPP’ là tam giác gì, tại sao ?b) Chứng minh rằng đường thẳng PQ luôn luôn tiếp xúc với đường tròn (O,OA).c) Chứng minh rằng đường tròn ngoại tiếp tam giác OPQ luôn luôn tiếp xúc với một đường thẳng cố định
Đọc tiếp
Cho đoạn thẳng AB với trung điểm O. Trên nửa mặt phẳng bờ AB kẻ các tia Ax, By vuông góc với
AB. Một góc vuông POQ quay xung quanh O cắt Ax, By tại P, Q. Gọi P’ là giao điểm của các tia đối
của các tia OP, By.
a) Tam giác QPP’ là tam giác gì, tại sao ?
b) Chứng minh rằng đường thẳng PQ luôn luôn tiếp xúc với đường tròn (O,OA).
c) Chứng minh rằng đường tròn ngoại tiếp tam giác OPQ luôn luôn tiếp xúc với một đường thẳng cố định
Cho đoạn thẳng AB với trung điểm O. Trên nửa mặt phẳng bờ AB kẻ các tia Ax, By vuông góc vớiAB. Một góc vuông POQ quay xung quanh O cắt Ax, By tại P, Q. Gọi P’ là giao điểm của các tia đốicủa các tia OP, By.a) Tam giác QPP’ là tam giác gì, tại sao ?b) Chứng minh rằng đường thẳng PQ luôn luôn tiếp xúc với đường tròn (O,OA).c) Chứng minh rằng đường tròn ngoại tiếp tam giác OPQ luôn luôn tiếp xúc với một đường thẳng cố định
Đọc tiếp
Cho đoạn thẳng AB với trung điểm O. Trên nửa mặt phẳng bờ AB kẻ các tia Ax, By vuông góc với
AB. Một góc vuông POQ quay xung quanh O cắt Ax, By tại P, Q. Gọi P’ là giao điểm của các tia đối
của các tia OP, By.
a) Tam giác QPP’ là tam giác gì, tại sao ?
b) Chứng minh rằng đường thẳng PQ luôn luôn tiếp xúc với đường tròn (O,OA).
c) Chứng minh rằng đường tròn ngoại tiếp tam giác OPQ luôn luôn tiếp xúc với một đường thẳng cố định