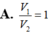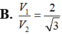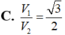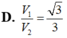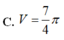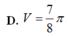Các câu hỏi tương tự
Cho tam giác đều ABC có diện tích
3
quay xung quanh cạnh AC, thể tích khối tròn xoay được tạo thành là A.
2
π
B.
π
C.
7
4
π
D.
7
8
π
Đọc tiếp
Cho tam giác đều ABC có diện tích 3 quay xung quanh cạnh AC, thể tích khối tròn xoay được tạo thành là
A. 2 π
B. π
C. 7 4 π
D. 7 8 π
Cho tam giác ABC vuông tại A. Đường thẳng d đi qua A và song song với BC. Cạnh BC quay xung quanh d tạo thành một mặt xung quanh của hình trụ có thể tích là V1. Tam giác ABC quay xung quanh trục d được khối tròn xoay có thể tích là V2. Tính tỉ số
V
1
V
2
.
Đọc tiếp
Cho tam giác ABC vuông tại A. Đường thẳng d đi qua A và song song với BC. Cạnh BC quay xung quanh d tạo thành một mặt xung quanh của hình trụ có thể tích là V1. Tam giác ABC quay xung quanh trục d được khối tròn xoay có thể tích là V2. Tính tỉ số V 1 V 2 .
![]()
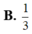
![]()
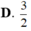
Trong không gian, cho tam giác ABC đều cạnh
a
. Tính thể tích V của khối tròn xoay nhận được khi quay tam giác ABC xung quanh trục BC.
Đọc tiếp
Trong không gian, cho tam giác ABC đều cạnh a . Tính thể tích V của khối tròn xoay nhận được khi quay tam giác ABC xung quanh trục BC.
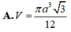
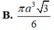
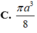
Ban đầu ta có một tam giác đều cạnh bằng 3 (hình 1). Tiếp đó ta chia mỗi cạnh của tam giác thành 3 đoạn bằng nhau và thay mỗi đoạn ở giữa bằng hai đoạn bằng nó sao cho chúng tạo với đoạn bỏ đi một tam giác đều về phía bên ngoài ta được hình 2. Khi quay hình 2 xung quanh trục d ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.
Đọc tiếp
Ban đầu ta có một tam giác đều cạnh bằng 3 (hình 1). Tiếp đó ta chia mỗi cạnh của tam giác thành 3 đoạn bằng nhau và thay mỗi đoạn ở giữa bằng hai đoạn bằng nó sao cho chúng tạo với đoạn bỏ đi một tam giác đều về phía bên ngoài ta được hình 2. Khi quay hình 2 xung quanh trục d ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.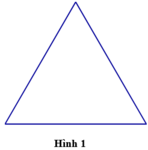

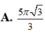
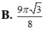
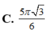
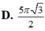
Trong không gian cho tam giác ABC là tam giác đều cạnh a. Gọi S là diện tích của mặt tròn xoay nhận được khi quay các cạnh AB và AC xung quanh trục BC. Tính S.
Đọc tiếp
Trong không gian cho tam giác ABC là tam giác đều cạnh a. Gọi S là diện tích của mặt tròn xoay nhận được khi quay các cạnh AB và AC xung quanh trục BC. Tính S.
![]()
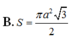
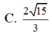
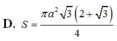
Cho tam giác ABC nội tiếp trong đường tròn tâm O, bán kính R có
B
A
C
^
75
0
,
A
C
B
^
60
0
. Kẻ
B
H
⊥
A
C
. Quay tam giác ABC quanh AC thì tma giác BHC tạo thành hình nón tròn xoa...
Đọc tiếp
Cho tam giác ABC nội tiếp trong đường tròn tâm O, bán kính R có B A C ^ = 75 0 , A C B ^ = 60 0 . Kẻ B H ⊥ A C . Quay tam giác ABC quanh AC thì tma giác BHC tạo thành hình nón tròn xoay (N). Tính diện tích xung quanh của hình nón xoay (N) theo R
A. 3 + 2 2 2 π R 2
B. 3 + 2 3 2 π R 2
C. 3 2 + 1 4 π R 2
D. 3 3 + 1 4 π R 2
Cho
∆
ABC vuông tại A có AB 3, AC 4. Quay tam giác quanh AB ta được hình nón tròn xoay có diện tích xung quanh
S
1
và quay tam giác quanh AC ta thu được hình nón xoay có diện tích xung quanh
S
2
. Tính tỉ số
S
1
S
2
A.
4
3...
Đọc tiếp
Cho ∆ ABC vuông tại A có AB = 3, AC = 4. Quay tam giác quanh AB ta được hình nón tròn xoay có diện tích xung quanh S 1 và quay tam giác quanh AC ta thu được hình nón xoay có diện tích xung quanh S 2 . Tính tỉ số S 1 S 2
A. 4 3
B. 3 4
C. 4 5
D. 3 5
Cho tam giác ABC có
A
B
C
^
90
°
,
A
C
B
^
30
°
,
A
B
2
2
. Quay tam giác ABC xung quanh cạnh BC ta được khối tròn xoay có thể tích V bằng:
Đọc tiếp
Cho tam giác ABC có A B C ^ = 90 ° , A C B ^ = 30 ° , A B = 2 2 . Quay tam giác ABC xung quanh cạnh BC ta được khối tròn xoay có thể tích V bằng:

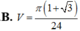
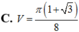
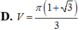
Cho tam giác vuông ABC với
B
^
60
°
(vuông tại A). Cho CB quay quanh CA tạo thành khối tròn xoay có thể tích
V
1
còn BC quay quanh BA tạo thành khối tròn xoay có thể tích
V
2
. Tính
V
1
V
2
.
Đọc tiếp
Cho tam giác vuông ABC với B ^ = 60 ° (vuông tại A). Cho CB quay quanh CA tạo thành khối tròn xoay có thể tích V 1 còn BC quay quanh BA tạo thành khối tròn xoay có thể tích V 2 . Tính V 1 V 2 .