\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\left|2\overrightarrow{AM}\right|=2AM\)\(\)(M là trung điểm BC)
\(=2AM=2\sqrt{AC^2-\left(\dfrac{BC}{2}\right)^2}=2\sqrt{a^2-\dfrac{a^2}{4}}=a\sqrt{3}\)
Cho tam giác ABC và M là trung điểm BC. Phân tích vec tơ AM theo vec tơ BA và vec tơ CA
Trên đường thẳng chứa cạnh BC của tam giác ABC lấy điểm M sao cho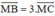 
. Hãy phân tích vec tơ 
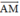theo hai vec tơ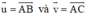 
Trên mặt phẳng tọa độ Oxy cho tam giác ABC có A(1;3) , B(-2;1) và C(0;3).
Vec tơ \(\overrightarrow{AB}+\overrightarrow{AC}\) có tọa độ là
Câu 1: Cho tam giác đều ABC có cạnh là 10a, M là trung điểm của BC. Tính | vec AB + vec AM | ? vec AM . vec BA ? Câu 2: Cho tam giác ABC vuông tại A có AB = 2a căn 3 ; AC = 2a . Tính ? vec AB . vec BC ; | vec AB - vec AC |
Cho hai vec tơ 
và {\displaystyle {\vec {d}}}
đều khác 
Gọi 
là góc giữa hai vec tơ đó.
Ta có 
Trong mặt phẳng tọa độ, các mệnh đề sau đúng hay sai?
a) a→ (-3; 0) và i→ (1; 0) là hai vec tơ ngược hướng.
b) a→ (3; 4) và b→ (-3; -4) là hai vec tơ đối nhau
c) a→ (5; 3) và b→ (3; 5) là hai vec tơ đối nhau.
d) Hai vec tơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.
cho hình thoi ABCD cạnh bằng a có tâm O, góc BAD =60 ĐỘ. tính độ dài vec tơ sau.
a) VECTO AB + VECTO AD.
b) VECTO AB - VECTO AC.
c)VECTO AB + VECTO AC.
d) VECTO AD + VECTO CB.
e) VECTO OB - VECTO DC
Cho AK và BM là hai trung tuyến của tam giác ABC. Hãy phân tích các vectơ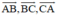 
theo hai vec tơ 
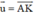và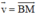 
Cho tam giác ABC có AB=4, AC = 5 , BAC =120°. G là trọng tâm của tam giác ABC, điểm E thỏa mãn vector AE=2/3 vector EC
a) Biểu diễn BE theo AB,AC.
b) Tìm tập hợp điểm I thỏa mãn đẳng thức vec tơ |IA+IG|=|IA–IG|.
c) M là một điểm khác G thỏa(GC-GB)(MA+MB+MC)=0. Chứng minh MG vg BC.
vector het nha
