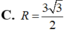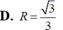Đáp án B
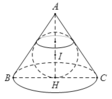
Mặt cầu nội tiếp hình nón đề cho có 1 đường trong lớn nội tiếp tam giác đều (cạnh a)
Nên mặt cầu đó có bán kính 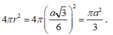
![]()
Vậy diện tích mặt cầu cần tìm là V = 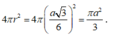
Đáp án B

Mặt cầu nội tiếp hình nón đề cho có 1 đường trong lớn nội tiếp tam giác đều (cạnh a)
Nên mặt cầu đó có bán kính 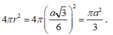
![]()
Vậy diện tích mặt cầu cần tìm là V = 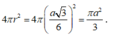
Câu 1. Cho hình chóp S ABC . có SA vuông góc với ABC và đáy ABC đều cạnh a. Biết SA=3a/2.Gọi H là trung điểm của BC.
a. Tính góc giữa hai mặt phẳng SBC và ABC ?
b. Tính diện tích của tam giác ABC từ đó suy ra diện tích tam giác SBC ?
c. Chứng minh SBC vuông góc với SAH
Câu 2. Cho hình chóp tam giác đều S ABC . có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số đo góc hợp bởi mặt bên và mặt đáy
Cho hình nón đỉnh S. Xét hình chóp S.ABC có đáy ABC là tam giác ngoại tiếp đường tròn đáy của hình nón và AB=BC=10a, AC=12a , góc tạo bởi hai mặt phẳng (SAB)) và (ABC) bằng 45 o C Thể tích khối nón đã cho bằng
A. 9 πa 3
B. 12 πa 3
C. 27 πa 3
D. 3 πa 3
Cho hình nón đỉnh S. Xét hình chóp S.ABC có đáy ABC là tam giác ngoại tiếp đường tròn đáy của hình nón và có AB= BC= 10a, AC= 12a, góc tạo bởi hai mặt phẳng(SAB) và ( ABC) bằng 60 0 . Tính thể tích khối nón đã cho.
A. 9 π a 3
B. 27 π a 3
C.3 π a 3
D. 12 π a 3
Cho tam giác đều ABC cạnh 1 và hình vuông MNPQ nội tiếp trong tam giác ABC(M ∈ AB, N ∈ AC, P,Q ∈ BC) . Gọi S là phần mặt phẳng chứa các điểm thuộc tam giác ABC nhưng không chứa các điểm thuộc hình vuông MNPQ. Thể tích của vật thể tròn xoay khi quay S quanh trục là đường thẳng qua A vuông góc với BC là:
A . 810 - 467 3 24 π
B . 4 3 - 3 96 π
C . 4 3 - 3 96
D . 54 - 31 3 12 π
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC), gọi I là trung điểm cạnh BC. Biết góc giữa đường thẳng SI và mặt phẳng (ABC) bằng 60 ° . Tính khoảng cách giữa hai đường thẳng SB và AC?
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại đỉnh B với AC =2a, BC =a. Đỉnh S cách đều các điểm A, B, C. Biết góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 60 o Khoảng cách từ trung điểm M của SC đến mặt phẳng (SAB) bằng
A. a 39 13
B. 3 a 13 13
C. a 39 26
D. a 13 26
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC); góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 60 o . Gọi M là trung điểm của cạnh AB. Tính khoảng cách d từ B đến mặt phẳng (SMC).
A. d = a 39 13
B. d = a 2
C. d = a
D. d = a 3
Cho tứ diện ABCD có hai mặt ABC và BCD là hai tam giác cân có chung đáy BC. Gọi I là trung điểm của cạnh BC.
a) Chứng minh rằng BC vuông góc với mặt phẳng (ADI)
b) Gọi AH là đường cao của tam giác ADI, chứng minh rằng AH vuông góc với mặt phẳng (BCD).
Cho hình nón có đường sinh bằng đường kính đáy và bằng 2. Bán kính của mặt cầu ngoại tiếp hình nón đó là
Trong không gian a và b có thể cắt nhau và cùng thuộc mặt phẳng song song với mặt phẳng đã cho.
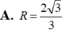
![]()