Dựng điểm D sao cho H là trung điểm AD.
Ta có; H là trung điểm của mỗi đường AD ; BC. Do đó, tứ giác ACDB là hình bình hành.
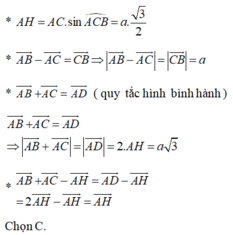
Dựng điểm D sao cho H là trung điểm AD.
Ta có; H là trung điểm của mỗi đường AD ; BC. Do đó, tứ giác ACDB là hình bình hành.
Cho tam giác ABC có ABC có A(2; 2; 1), B(4; 4; 2), C(-2; 4; -3). Vectơ nào dưới đây là vectơ chỉ phương của đường phân giác trong AD của tam giác ABC.
A. - 2 ; 4 ; - 3
B. 6 ; 0 ; 5
C. 0 ; 1 ; - 1 3
D. - 4 3 ; - 1 3 ; - 1
Cho tam giác ABC có góc B tù và H là chân đường cao của tam giác hạ từ đỉnh A. Cặp vectơ nào sau đây cùng hướng?
A. B H → , C H →
B. B H → , B C →
C. B H → , H C →
D. C H → , H B →
Trong một mặt phẳng oxy cho A (4;6) b (1;4) c (7; 3/2) A. Chứng minh tam giác ABC vuông tại a B. Tính độ dài cạnh ab Có. Tính góc giữa hai vectơ a' b' biết a = (1;2) b (1;3)
Tam giác ABC vuông tại A có đường cao AH = h và có BC = a, CA = b, AB = c. Gọi BH = c’ và CH = b’(h.2.11). Hãy điền vào các ô trống trong các hệ thức sau đây để được các hệ thức lượng trong tam giác vuông:
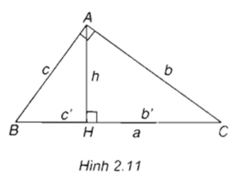
a2 = b2 + (.....)
b2 = a x (.....)
c2 = a x (.....)
h2 = b’ x (.....)
ah = b x (.....)
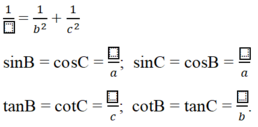
Câu 21: Cho tam giác ABC với AD là đường phân giác trong. Biết AB = 5 , BC = 6 , CA = 7 . Khẳng định nào sau đây Đúng? A, vectơ AD = 5/12 vectơ AB + 7/12 vectơ AC B, vectơ AD = 7/12 vectơ AB - 5/12 vectơ AC C, vectơ AD = 7/12 vectơ AB + 5/12 vectơ AC D, vectơ AD = 5/12 vectơ AB - 7/12 vectơ AC
Cho tam giác $A B C$ vuông tại $A$ có $A B C=30^{\circ}$ và $B C=a \sqrt{5}$.
Tính độ dài của các vectơ $\overrightarrow{A B}+\overrightarrow{B C}, \overrightarrow{A C}-\overrightarrow{B C}$ và $\overrightarrow{A B}+\overrightarrow{A C}$.
Bài 10:Cho ABC có a = 8, b =10, c =13 a. ABC có góc tù hay không ? Tính bán kính đường tròn ngoại tiếp ABC. b. Tính diện tích ABC
Bài 11:Cho tam giác ABC có: a = 6, b = 7, c = 5. a) Tính S ,h ,R,r ABC a b) Tính bán kính đường tròn đi qua A, C và trung điểm M của cạnh AB.
Bài 12:Cho tam giác ABC có: AB = 6, BC = 7, AC = 8. M trên cạnh AB sao cho MA = 2 MB. a) Tính các góc của tam giác ABC. b) Tính S ,h ,R ABC a , r. c) Tính bán kính đường tròn ngoại tiếp ∆MBC.
Bài 13:Cho ABC có 0 0 A B b = = = 60 , 45 , 2 tính độ dài cạnh a, c, bán kính đường tròn ngoại tiếp và diện tích tam giác ABC
Bài 14:Cho ABC AC = 7, AB = 5 và 3 cos 5 A = . Tính BC, S, a h , R, r.
Bài 15:Cho ABC có 4, 2 m m b c = = và a =3 tính độ dài cạnh AB, AC.
Bài 16:Cho ABC có AB = 3, AC = 4 và diện tích S = 3 3 . Tính cạnh BC
Bài 17:Cho tam giác ABC có ˆ o A 60 = , c h 2 3 = , R = 6. a) Tính độ dài các cạnh của ∆ABC. b) Họi H là trực tâm tam giác ABC. Tính bán kính đường tròn ngoại tiếp ∆AHC.
Bài 18:a. Cho ABC biết 0 0 a B C = = = 40,6; 36 20', 73 . Tính BAC , cạnh b,c. b.Cho ABC biết a m = 42,4 ; b m = 36,6 ; 0 C = 33 10' . Tính AB, và cạnh c.
Bài 19:Tính bán kính đường tròn nội tiếp ABC biết AB = 2, AC = 3, BC = 4.
Bài 20:Cho ABC biết A B C (4 3; 1 , 0;3 , 8 3;3 − ) ( ) ( ) a. Tính các cạnh và các góc của ABC b. Tính chu vi và diện tích ABC
Cho các mệnh đề :
A : “Nếu tam giác ABC đều có cạnh bằng a, đường cao là h thì h = a 3 2 ”
B : “Tứ giác có bốn cạnh bằng nhau là hình vuông”
C : “15 là số nguyên tố”
D : “ 225 là một số nguyên”
Chọn câu sai:
A. Mệnh đề A => B sai
B. Mệnh đề A ⇔ D đúng
C. Mệnh đề B ⇔ C đúng
D. Mệnh đề => D sai
Cho tam giác ABC với các đường cao ha,hb,hc;a,b,c lần lượt là độ dài các cạnh BC,CA,AB . Chứng minh rằng :
\(\frac{a}{h_a}+\frac{b}{h_b}+\frac{c}{h_c}\ge2\left(tan\frac{A}{2}+tan\frac{B}{2}+tan\frac{C}{2}\right)\)