Các câu hỏi tương tự
Cho tam giác ABC vuông tại A, gọi E là trung điểm BC, kẻ EF vuông góc AB, EI vuông góc AC (F thuộc AB, I thuộc AC)
a) C/m AFEI là hình chữ nhật
b) c/m BFIE là hình bình hành
c) Gọi K là điểm thuộc đoạn thẳng AC (K khác A và I), kẻ ID vuống góc với FK (D thuộc FK)
Chứng minh ED vuông góc AD
Cho tam giác DEF có DE=5cm, DF=9cm, DI là đường phân giác ( I thuộc EF ). Kẻ EM, FN vuông góc với DI. Qua trung điểm K của EF kẻ đường thẳng song song với DI cắt DF tại H, cắt ED tại C. Chứng minh EC=FH.
Xem chi tiết
cho tam giác DEF vuông tại D trên tia đối của tia DE lấy A , kẻ AB vuông góc với EF , qua F kẻ đường thẳng vuông góc với EF cắt ED tại Q , AF tại K , DK lần lượt cắt AI , QF tại M , N chứng minh rằng N là trung điểm của FQ
cho tam giác ABC vuông tại A , AH là dường cao . kẻ HE và HF lần lượt vuông góc với AB và AC
a, chứng minh AH=EF
b, gọi O là giao điể của AH và EF , K là trung điểm của AC , qua F kẻ đường thẳng vuông góc với EF cắt BC tại I. chứng minh AOIK là hbh
c, EF cắt Ik tại M chứng minh OMI cân
p/s vẽ hình hộ e nha
Cho tam giác ABC vuông tại A, AH là đường cao (H thuộc BC). Kẻ HE, HF lần lượt vuông góc với AB và AC (E thuộc AB, F thuộc AC). a)Chứng minh AH=EF.
b)Gọi O là giao điểm của AH và EF, K là trung điểm của AC. Qua F kẻ đường thẳng vuông góc với EF cắt BC ở I. Chứng minh tứ giác AOIK là hình bình hành
cho tam giác ABC vuông tại A có trung tuyến AM .Kẻ AH vuông góc vs AB ,MK vuông góc vs AC
a, c/m tứ giác AKMH là hcn
b, E là trung điểm của MH. c/m 3 điểm B,E,K thẳng hàng
c, gọi F là trung diểm của MK .Đường thẳng HK cắt AE tại I và AF tại I và AF tại j .c/m HI=KJ
C1:Cho tam giác ABC có trung AM tuyến. gọi E là điểm đối xứng A qua Ma) nếu tam giác ABC cân tại A thì tứ giác ABEC là hình gì? vì sao?b) Tìm điều kiện của tam giác ABC để tứ giác ABEC là hình vuông hình vuông.C2: cho tam giác DEF vuông ở D và điểm H di động trên cạnh EF kẻ HI ông góc với DE (I thuộc DE) kẻ HK vuông góc với DF (K thuộc DF)a) chứng minh rằng DHIKb) xác định vị trí của điểm H Trên cạnh EF sao cho IK có độ dài nhỏ nhấtc) xác định vị trí của điểm H Trên cạnh EF để tứ giác DIHK là hì...
Đọc tiếp
C1:
Cho tam giác ABC có trung AM tuyến. gọi E là điểm đối xứng A qua M
a) nếu tam giác ABC cân tại A thì tứ giác ABEC là hình gì? vì sao?
b) Tìm điều kiện của tam giác ABC để tứ giác ABEC là hình vuông hình vuông.
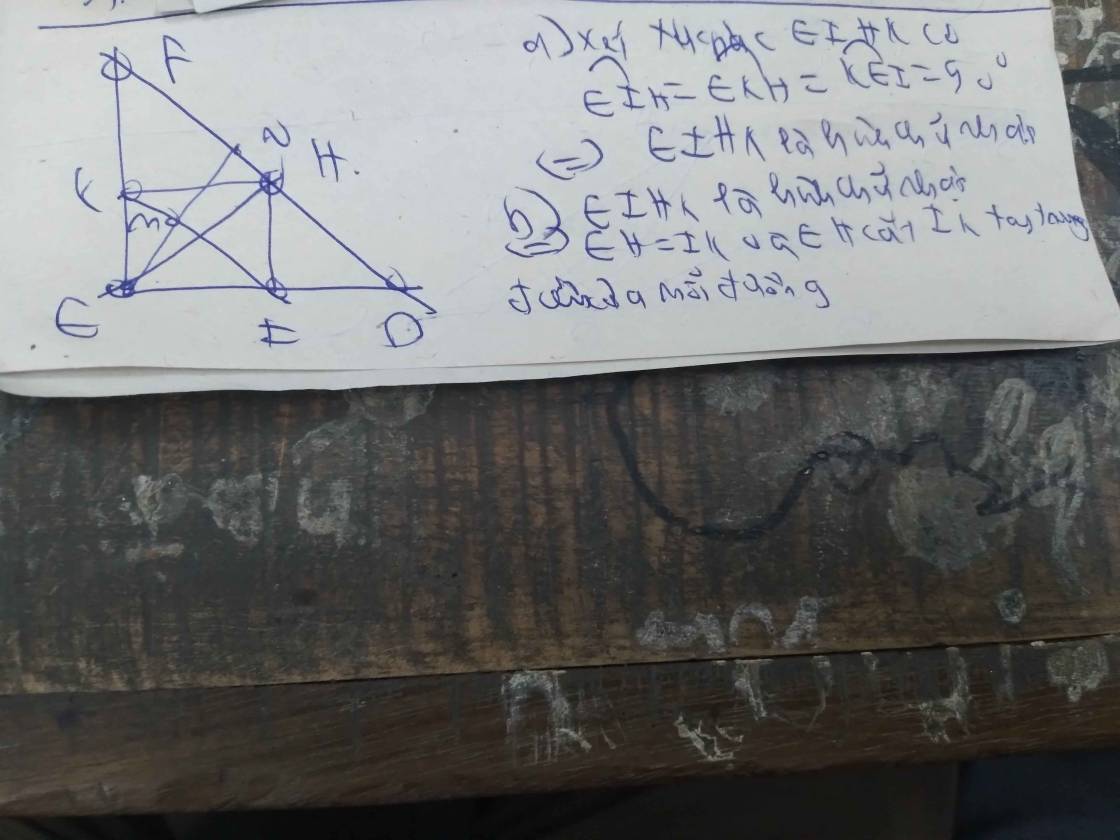
C2: cho tam giác DEF vuông ở D và điểm H di động trên cạnh EF kẻ HI ông góc với DE (I thuộc DE) kẻ HK vuông góc với DF (K thuộc DF)
a) chứng minh rằng DH=IK
b) xác định vị trí của điểm H Trên cạnh EF sao cho IK có độ dài nhỏ nhất
c) xác định vị trí của điểm H Trên cạnh EF để tứ giác DIHK là hình vuông
Mong mọi người giúp đỡ !!!!
Cho tam giác ABC vuông tại A, AH là đường cao ( H thuộc BC). Kẻ HE, HF lần lượt vuông góc với AB và AC (E thuộc AB, F thuộc AC).
a) Chứng minh AH = EF.
b) Gọi O là giao điểm của AH và EF, K là trung điểm của AC. Qua F kẻ đường thẳng vuông góc với EF cắt BC tại I.Chứng minh tứ giác AOIK là hình bình hành.
c) EF cắt IK tại M. Chứng minh tam giác OMI cân
Cho tam giác DEF có DI là phân giác của góc D; I thuộc EF, ED=10 cm , DF=6 cm , FI= 4,8 cm.
a) Tính EI
b) Qua I kẻ đường thẳng song song với DF cắt DE tại M. Tính ME;MD;IM
c) Chứng minh: DE/DF = ME/MD
d) Gọi N là trung điểm của DF; DI cắt MN tại K; FM cắt IN tại H.Chứng minh: KH//MI